Мы живём в десятичной (decimal, DEC) системе счисления - любое число в ней можно представить десятью цифрами - от 0 до 9. Процессор же - цифровое устройство, то есть может оперировать только двумя величинами: 0 и 1, правда и ложь, высокий сигнал и низкий. Такая система счисления называется двоичной или бинарной (binary, BIN). Вся работа и процессор в целом построены на двоичной логике и многие моменты в программировании тоже на этом завязаны.
Единицы измерения информации #
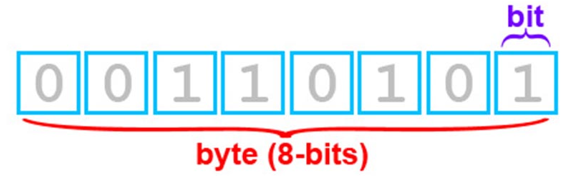
Единица измерения цифровой информации, которая имеет только два состояния, называется бит (bit). Соответственно элементарная ячейка памяти, с которой процессор может взаимодействовать - один бит. Как и в других единицах измерения, в цифровых величинах существуют приставки для упрощения счёта больших чисел (метр, сантиметр, километр...), но работают они с другими множителями. Следующая после бита единица измерения - байт (byte) - содержит 8 бит. Так сложилось исторически по ряду причин и в большинстве современных систем используется именно 8-битный байт, тогда как в некоторых старых системах он был 6, 7 или даже 9:
- Процессор работает с двоичными данными, поэтому аппаратно проще и удобнее реализовать адресацию по степеням двойки, то есть числа 2, 4, 8, 16, 32...
- 8 бит (256 значений) достаточно для хранения символа из стандартной таблицы символов
Следующие по объёму единицы измерения имеют привычные приставки кило-мега-гига-тера, но множитель у них - 1024, что привело к путанице с привычным множителем 1000. В 1999 году Международная электротехническая комиссия (МЭК) ввела стандарт по именованию двоичных чисел (IEC 60027-2 и позже IEC 80000-13), который предписывает считать множителями двоичных чисел кило-мега-гига-тера именно 1000. Для двоичных чисел были придуманы специальные приставки: киби-меби-гиби-теби с множителем 1024. Помимо величин с окончанием байт также есть вариант с окончанием бит, то есть указывает непосредственно на количество бит информации.
Таблицы с величинами
| Название | Объём |
|---|---|
| Килобайт, Кбайт, КБ (KByte, KB) | 1000 Байт, 10^3 Байт |
| Мегабайт, Мбайт, МБ (MByte, MB) | 1000 Кбайт, 10^6 Байт |
| Гигабайт, Гбайт, ГБ (GByte, GB) | 1000 Мбайт, 10^9 Байт |
| Терабайт, Тбайт, ТБ (TByte, TB) | 1000 Гбайт, 10^12 Байт |
| Название | Объём |
|---|---|
| Кибибайт, КиБ (KiB) | 1024 Байт, 2^10 Байт |
| Мебибайт, МиБ (MiB) | 1024 КиБ, 2^20 Байт |
| Гибибайт, ГиБ (GiB) | 1024 МиБ, 2^30 Байт |
| Тебибайт, ТиБ (TiB) | 1024 ГиБ, 2^40 Байт |
| Название | Объём |
|---|---|
| Килобит, кбит (kbit) | 10^3 бит |
| Мегабит, Мбит (Mbit) | 10^6 бит |
| Гигабит, Гбит (Gbit) | 10^9 бит |
| Терабит, Тбит (Tbit) | 10^12 бит |
| Название | Объём |
|---|---|
| Кибибит, Кибит (Kibit) | 1024 бит, 2^10 бит |
| Мебибит, Мибит (Mibit) | 1024 Кибит, 2^20 бит |
| Гибибит, Гибит (Gibit) | 1024 Мибит, 2^30 бит |
| Тебибит, Тибит (Tibit) | 1024 Гибит, 2^40 бит |
В то же время, в Российском стандарте от 2009 года принято использование множителя 1024 со стандартными приставками, то есть:
- 1 Кбайт = 1024 байт
- 1 Мбайт = 1024 Кбайт
- 1 Гбайт = 1024 Мбайт
- 1 Тбайт = 1024 Гбайт
Таким образом, для определения точного объёма информации необходимо учитывать контекст.
Двоичная система #
Если считать числа по порядку в любой системе счисления с шагом в 1, то, когда младший разряд достигает своего максимального значения - он становится 0, а старший для него разряд получает +1. Так, например, десятичное число 19 превращается в 20 после прибавления единицы - 9 становится нулём 0, а единица 1 прибавляется к следующему разряду и получается 2. Давайте посчитаем числа по порядку в десятичной и двоичной системах:
| DEC | BIN |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| … | … |
| 16 | 10000 |
Заметили последовательность?
Также здесь можно заметить особенность степени двойки - на ней в программировании завязано очень многое. Давайте посмотрим отдельно на первые 8 степеней двойки:
| 2^ | DEC | BIN |
|---|---|---|
| 0 | 1 | 00000001 |
| 1 | 2 | 00000010 |
| 2 | 4 | 00000100 |
| 3 | 8 | 00001000 |
| 4 | 16 | 00010000 |
| 5 | 32 | 00100000 |
| 6 | 64 | 01000000 |
| 7 | 128 | 10000000 |
Таким образом, степень двойки "указывает" на порядковый номер бита. Это можно использовать для перевода чисел из двоичной системы в десятичную - достаточно заменить каждую единичку на соответствующее ей значение и все их сложить. Например 1001 - это 2^3 + 2^0 = 8 + 1 = 9.
MSB и LSB #
Как и в любой другой системе счисления, у чисел в двоичной системе есть разряды. В жизни мы записываем числа слева направо, от старшего к младшему, то есть у десятичного числа 123 старшим разрядом будет 1, а младшим - 3. То же самое - с двоичным, для краткости самый младший разряд называется LSB (Least Significant Bit), а самый старший - MSB (Most Significant Bit): MSB -> 1001 <- LSB.
Эти обозначения довольно часто встречаются при работе с хранением и передачей данных: данные читаются и передаются по одному биту по порядку, но направление может быть разным! Если передача начинается со старшего бита - она называется MSB first (сначала MSB), если с младшего - LSB first (сначала LSB)
Другие системы счисления #
Система счисления может иметь любое основание, то есть можно представить себе троичную, пятеричную и любые другие системы.
Данные в памяти микроконтроллера хранятся в двоичном представлении, но компилятор поддерживает и другие системы, в которых мы можем работать - десятичная (decimal, DEC), восьмеричная (octal, OCT) и шестнадцатеричная (hexadecimal, HEX).
У систем счисления, отличных от десятичной, при записи чисел в коде программы требуется префикс - чтобы компилятор понимал, о чём идёт речь:
| Основание | Префикс | Значения | Пример |
|---|---|---|---|
| 2 (BIN) | 0b |
0-1 | 0b0101001 |
| 8 (OCT) | 0 (ноль) |
0–7 | 0175 |
| 10 (DEC) | нет | 0-9 | 100500 |
| 16 (HEX) | 0x |
0-9, буквы A-F и a-f | 0x0FF21A |
Переводить числа из одной системы счисления в другую не нужно - компилятор сделает это сам.
// одно и то же число
0b010011010010; // BIN
1234; // DEC
02322; // OCT
0x4D2; // HEXПоддержка разных систем счисления нужна просто для удобства программиста:
- Привычные
DECчисла мы будем использовать для обычных "человеческих" математических операций HEXчислами принято записывать цвет, адреса в памяти, а также всякие ключи шифрования, хэши и прочие численные коды - HEX визуально занимает меньше места и выглядит как некий "код". Ещё одно большое преимущество HEX - два соседних разряда занимают 1 байт, то есть визуально можно оценить размер числа и увидеть значение каждого байта в нём. Например0x12ab- это два байта со значениями0x12и0xabBINчисла удобно использовать для манипуляций с битами в числе, работы с регистрами и создания алгоритмов на базе битовой математикиOCTчисла на практике встречаются редко
Значащие нули #
Значащие нули – это нули, которые нельзя убрать из числа, иначе получится другое число. Например если из числа 1230 убрать правый ноль - оно уменьшится в 10 раз. По сути это крайние младшие разряды, находящиеся справа. Незначащие нули можно убрать или добавить к числу слева (сразу после префикса, если он имеется) - число от этого не изменится: если из числа 0b0011 убрать левый ноль - его значение останется 0b011, можно и второй ноль убрать - 0b11 - это всё ещё то же число. В предыдущих таблицах я добавил незначащих нулей числам в столбце BIN, чтобы выровнять их по количеству разрядов для наглядности.
Таким образом восьмеричная система - это ловушка Джокера. У числа есть незначащий ноль, убирать который нельзя!
Дополнительно #
Дополнительный контент доступен владельцам набора GyverKIT и по подписке, подробнее читай здесь. Блок содержит:
- Тезисы, Примеры (Arduino)
- 1 блоков кода
Полезные страницы #
- Набор GyverKIT – наш большой стартовый набор Arduino, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])
- Поддержать автора за работу над уроками