Вернёмся к примеру с плавным асинхронным миганием светодиода/ленты на 3 пине:
void setup() {
pinMode(3, OUTPUT);
}
uint32_t tmr;
int val = 0;
bool dir = true;
void loop() {
if (millis() - tmr >= 20) {
tmr = millis();
if (dir) val++; // увеличиваем яркость
else val--; // уменьшаем
if (val >= 255 || val <= 0) dir = !dir; // разворачиваем
analogWrite(3, val);
}
}Если вы соберёте схему и загрузите пример, то увидите, что яркость меняется неравномерно, нелинейно.
Гамма #
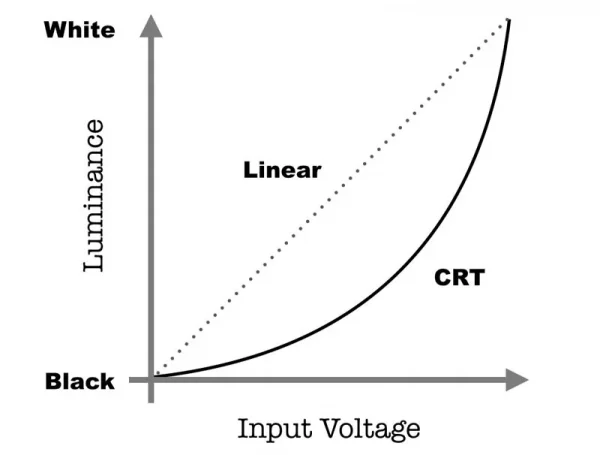
Дело в том, что человеческий глаз воспринимает яркость экспоненциально и для улучшения восприятия мигающего светодиода ШИМ сигнал тоже надо менять нелинейно, по так называемой гамме, т.е. сделать гамма-коррекцию (Википедия). Такое преобразование появилось на ЭЛТ (CRT) мониторах, чтобы преобразовать "математическую" яркость пикселя в "человеческую", поэтому гамма часто называется CRT-гаммой. На следующем графике по вертикальной оси - светимость, по горизонтальной - условное напряжение:
Как задать изменение ШИМ сигнала (яркость) по такому закону? Есть несколько способов, давайте обо всём по порядку.
Данный урок не даёт сразу готового идеального решения - это цепочка рассуждений и рассмотрение нескольких вариантов и алгоритмов, приведение от сложного и каноничного к простому и эффективному. Если вам нужно готовое решение - читайте сразу самый конец, про кубическую параболу. Если вам интересен ход мысли и развитие кода - внимательно читайте весь урок!
Степенное уравнение #
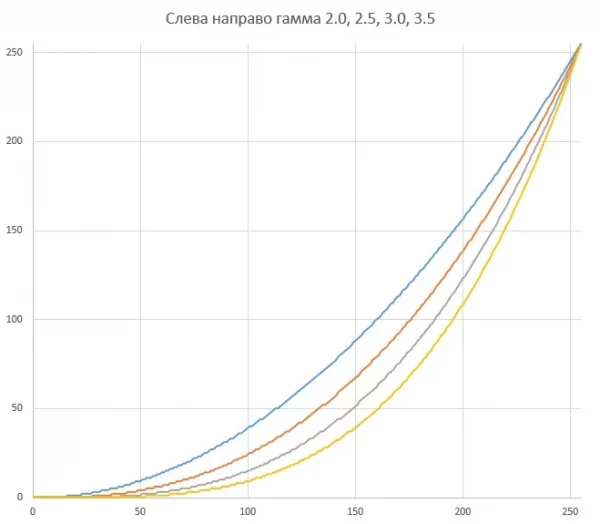
В основе лежит уравнение вида out = (max / (max^gamma)) * (val^gamma), (также можно встретить вариант out = max * ((val / max) ^ gamma)), где val - "обычное" значение для ШИМ, out - новое, скорректированное, max - максимальное значение для val, а gamma - коэффициент коррекции гаммы, обычно принимается в диапазоне 2.0-3.0. На графике перехода обычного сигнала (горизонтальная ось) в скорректированный (вертикальная ось) это выглядит так:
В принципе этим уравнением уже можно пользоваться, возьмём наш пример с плавно мигающим светодиодом и добавим в него функцию для перевода "линейного" ШИМ с гаммой для примера 2.46. Также я заранее посчитал первую скобку (для первого уравнения) (255.0 / pow(255, 2.46)), потому что её значение меняться не будет:
void setup() {
pinMode(3, OUTPUT);
}
// функция возвращает скорректированное по CRT значение
byte getBrightCRT(byte val) {
return (0.0003066 * pow(val, 2.46));
}
uint32_t tmr;
int val = 0;
bool dir = true;
void loop() {
if (millis() - tmr >= 20) {
tmr = millis();
if (dir) val++; // увеличиваем яркость
else val--; // уменьшаем
if (val >= 255 || val <= 0) dir = !dir; // разворачиваем
analogWrite(3, getBrightCRT(val));
}
}Для 10 бит ШИМ формула будет такая: 0.000040326 * pow(val, 2.46)
Если теперь попробовать менять яркость реального светодиода, вы увидите разницу: изменение яркости стало более приятным глазу! Чем хорош данный способ? Он позволяет выбрать гамму с любой точностью, и это его единственный плюс. Из-за использования дробных степеней (функция pow()) вся функция выполняется очень долго, в районе 400 мкс, а также требует подключения библиотеки для таких вычислений, что прибавляет программе аж 2 килобайта Flash! То есть в два раза больше, чем есть например в ATtiny13. Попробуем оптимизировать.
Таблица #
В программировании часто используется табличный подход: если существует фиксированный набор значений вычисления уравнения, то его можно посчитать заранее, сохранить как массив и использовать готовый результат напрямую. Давайте запишем результаты предыдущего уравнения для диапазона 0-255 и сохраним в PROGMEM. Таким образом получим 256 байт в памяти вместо 2 кБ расчётов.
// гамма-таблица
const uint8_t CRTgammaPGM[256] PROGMEM = {
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1,
1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8,
8, 8, 9, 9, 9, 10, 10, 10, 11, 11, 12, 12, 12, 13, 13, 14,
14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19, 20, 20, 21, 21, 22,
23, 23, 24, 24, 25, 26, 26, 27, 28, 28, 29, 30, 30, 31, 32, 32,
33, 34, 35, 35, 36, 37, 38, 39, 39, 40, 41, 42, 43, 44, 45, 45,
46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61,
62, 63, 64, 65, 66, 68, 69, 70, 71, 72, 73, 74, 76, 77, 78, 79,
81, 82, 83, 84, 86, 87, 88, 90, 91, 92, 94, 95, 96, 98, 99, 101,
102, 103, 105, 106, 108, 109, 111, 112, 114, 115, 117, 118, 120, 122, 123, 125,
126, 128, 130, 131, 133, 135, 136, 138, 140, 142, 143, 145, 147, 149, 150, 152,
154, 156, 158, 160, 161, 163, 165, 167, 169, 171, 173, 175, 177, 179, 181, 183,
185, 187, 189, 191, 193, 195, 197, 200, 202, 204, 206, 208, 210, 213, 215, 217,
219, 221, 224, 226, 228, 231, 233, 235, 238, 240, 242, 245, 247, 250, 252, 255,
};
void setup() {
pinMode(3, OUTPUT);
}
// функция возвращает скорректированное по CRT значение
byte getBrightCRT(byte val) {
return pgm_read_byte(&(CRTgammaPGM[val]));
}
uint32_t tmr;
int val = 0;
bool dir = true;
void loop() {
if (millis() - tmr >= 20) {
tmr = millis();
if (dir) val++; // увеличиваем яркость
else val--; // уменьшаем
if (val >= 255 || val <= 0) dir = !dir; // разворачиваем
analogWrite(3, getBrightCRT(val));
}
}При помощи таблицы можно выводить любую гамму, заранее её посчитав. А как быть с 10 битами? Таблица займёт 1024*2, то есть 2 килобайта! Для 10 бит таблица будет неоправданно много "весить", пусть даже доступ к таблице в сотни раз быстрее вычислений: около 0.8 микросекунды!
// ещё одна таблица
const uint8_t CRTgammaPGM[256] PROGMEM = {
0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 5,
5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 8,
9, 10, 10, 10, 10, 11, 11, 12, 12, 12, 12, 13, 13, 13, 14, 14,
15, 15, 15, 16, 17, 17, 17, 17, 18, 18, 19, 20, 20, 20, 20, 21,
22, 22, 23, 23, 23, 24, 25, 25, 26, 26, 27, 27, 28, 28, 29, 30,
30, 31, 31, 32, 33, 33, 34, 35, 35, 36, 37, 37, 38, 38, 39, 40,
41, 41, 42, 43, 44, 45, 45, 46, 47, 47, 48, 49, 50, 51, 52, 53,
54, 54, 55, 56, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 69, 70, 71, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 84,
85, 86, 87, 89, 90, 91, 93, 94, 95, 96, 97, 98, 100, 101, 102, 103,
105, 106, 108, 109, 110, 111, 113, 115, 117, 118, 119, 121, 122, 123, 124, 127,
128, 130, 131, 133, 134, 136, 137, 139, 140, 143, 145, 146, 147, 148, 151, 153,
154, 156, 158, 159, 162, 163, 165, 167, 169, 171, 173, 174, 176, 179, 180, 182,
185, 186, 188, 190, 192, 194, 196, 199, 201, 202, 205, 207, 209, 211, 214, 216,
218, 220, 223, 225, 226, 230, 231, 235, 236, 240, 241, 245, 246, 250, 251, 255,
};Полином #
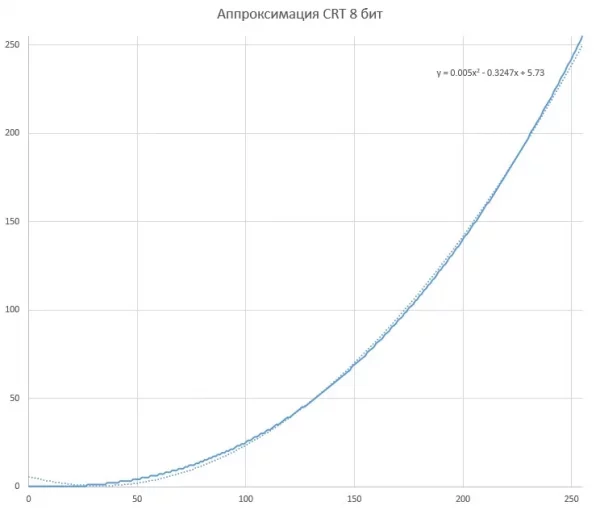
Что ещё можно сделать с графиком, чтобы его "запомнить" в памяти? Правильно, попробовать заменить его более простой функцией. Загнав таблицу в Excel и построив линию тренда видим, что гамма вполне сносно аппроксимируется полиномом, который гораздо проще вычислить:
Расхождения появляются в нижней части, но их можно обойти при помощи условия: если меньше начального значения, то считать результат нулём. Итоговая функция с чуть подправленным уравнением:
// функция возвращает скорректированное по CRT значение
// для 8 бит ШИМ
byte getBrightCRT(byte val) {
return ((i > 23) ? (0.00512 * val * val - 0.325 * val + 5.73) : 0);
}
// функция возвращает скорректированное по CRT значение
// для 10 бит ШИМ
int getBrightCRT(int val) {
return ((i > 112) ? (0.00127 * val * val - 0.321 * val + 23.0) : 0);
}Мы не сильно потеряли в точности кривой, но зато сильно ускорили и облегчили код: перевод выполняется за 56 микросекунд, а во Flash памяти занимает ~1 килобайт за счёт использования float. Если он используется где-то ещё в коде, дополнительно память практически не займётся. Также способ является универсальным для любой битности и гаммы. Но можно пойти ещё дальше!
Парабола x^2 #
Если принять gamma равной 2, при которой график всё ещё весьма далёк от линейного и всё ещё отлично работает, то можно заметить (и по графику, и по функции), что это обычная парабола x*x. Таким образом формула упрощается до out = (long)val * val / maxOut, где maxOut будет двойкой в степени, а как мы знаем из урока по оптимизации, деление на такие вещи можно заменить сдвигом. Формула примет вид out = ((long)val * val) >> bit, где bit - разрядность ШИМ. Такое уравнение приведёт к тому, что результат не достигнет максимума на единицу (потеряется при делении). Для округления в большую сторону отлично работает такая конструкция out = ((long)(val + 1) * val) >> bit:
// квадратная гамма для 8 бит
uint8_t crt2_8(uint8_t val) {
return ((uint32_t)(val + 1) * val) >> 8;
}
// квадратная гамма для 10 бит
uint16_t crt2_10(uint16_t val) {
return ((uint32_t)(val + 1) * val) >> 10;
}И всё! Можно подставить её в предыдущий "полный" пример с миганием светодиода и наслаждаться. А что по скорости и весу? Всё очень круто, потому что мы используем целочисленные вычисления и даже не используем деление: расчёт выполняется за 4 микросекунды, а занимает всего 150 байт.
Парабола x^3 #
Точно так же можно подставить gamma = 3 в исходное степенное уравнение и получить упрощение до кубической параболы, которая будет вычисляться чуточку медленнее обычной, но результат будет более приятен глазу!
// кубическая гамма для 8 бит
uint8_t crt3_8(uint8_t val) {
return ((uint32_t)(val + 1) * (val + 1) * val) >> 16;
}
// кубическая гамма для 10 бит
uint16_t crt3_10(uint16_t val) {
return ((uint32_t)(val + 1) * (val + 1) * val) >> 20;
}Что использовать? #
Промежуточные выводы были сделаны в каждом способе, вот общая таблица для преобразования 8 бит ШИМ:
| Уравнение | Выполнение, мкс (при 16 МГц) | Flash память, байт |
|---|---|---|
| Степенное | 365 | 1920 |
| Полином | 56 | 960 |
| Парабола кубическая | 16 | 170 |
| Парабола квадратная | 4 | 152 |
| Таблица | 0.8 | 360 |
В общем случае рекомендуется использовать параболическую гамму как самую оптимальную по памяти и скорости выполнения (кубическая парабола приятнее воспринимается глазом, чем квадратная), а также с лёгкостью вместится даже в тиньку13.
Полезные страницы #
- Набор GyverKIT – наш большой стартовый набор Arduino, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])
- Поддержать автора за работу над уроками