Фильтрация сигналов
Шум при измерениях
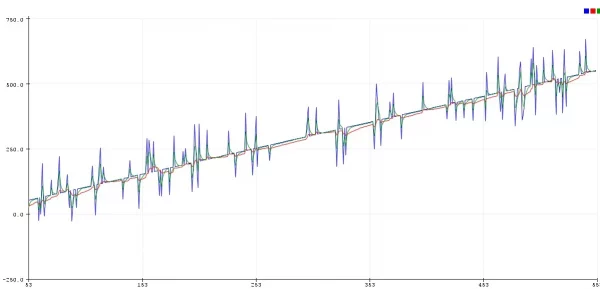
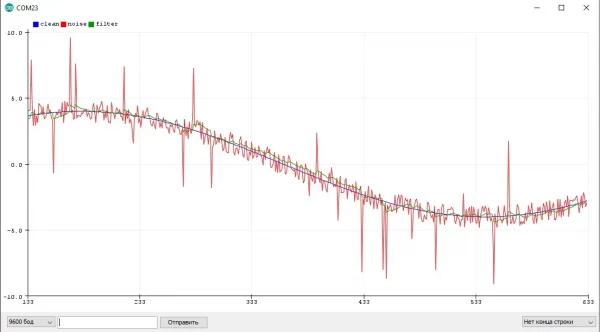
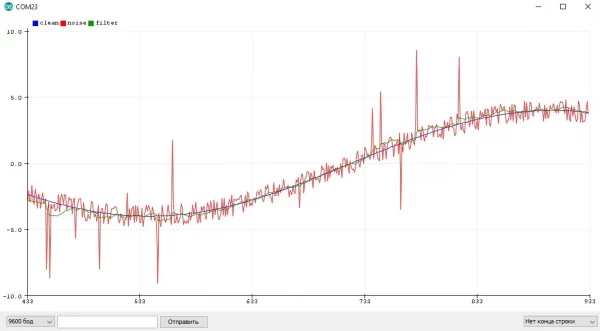
Шум можно условно разделить на два типа: постоянный шум датчика с одинаковым отклонением (скриншот 1), и случайный шум, который возникает при различных случайных (чаще всего внешних) обстоятельствах (скриншот 2). 
Небольшой шум наблюдается у любого аналогового датчика, который опрашивается средствами АЦП Ардуино. Причем сам АЦП практически не шумит, если обеспечить качественное питание платы и отсутствие электромагнитных наводок – сигнал с того же потенциометра будет идеально ровный. Но как только питание становится некачественным, например от дешёвого блока питания, картина меняется. Или, например, без нагрузки блок питания даёт хорошее питание и шума нет, но как только появляется нагрузка – вылезают шумы, связанные с устройством блока питания и отсутствием нормальных выходных фильтров. Или другой вариант – где то рядом с проводом к аналоговому датчику появляется мощный источник электромагнитного излучения (провод с большим переменным током), который наводит в проводах дополнительную ЭДС и мы опять же видим шум. Да, от этих причин можно избавиться аппаратно, добавив фильтры по питанию и экранировав все аналоговые провода, но это не всегда получается и поэтому в этом уроке мы поговорим о программной фильтрации значений.
Измерение значений
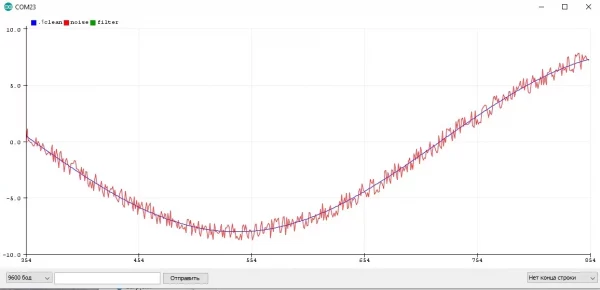
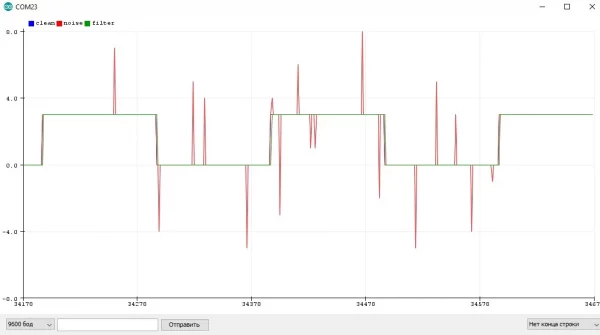
Давайте посмотрим, как измеряется сигнал в реальном устройстве. Естественно это происходит не каждую итерацию loop, а например по какому то таймеру. Представим что синий график отражает реальный процесс, а красный – измеренное значение с некоторым периодом. 
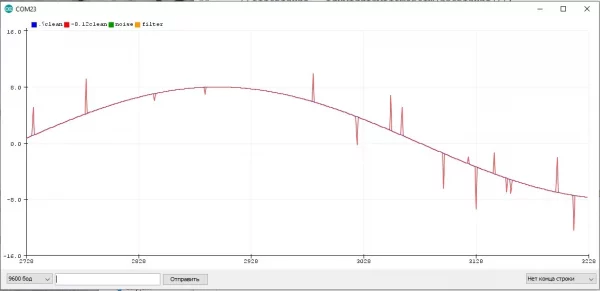
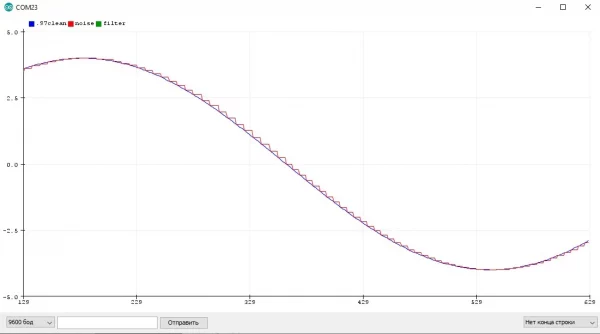
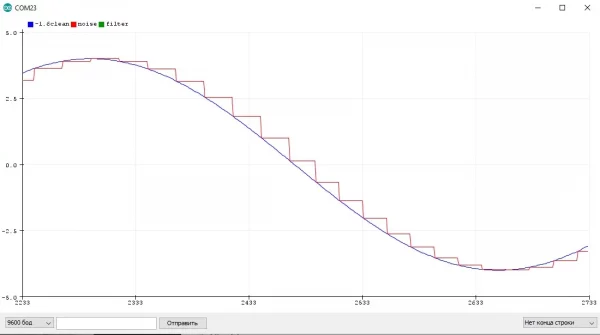
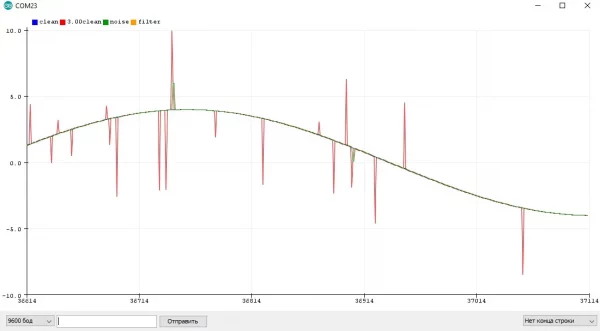
Я думаю очевидно, что между периодами измерения значения измеренное значение не меняется и остаётся постоянным, что видно из графика. Давайте увеличим период и посмотрим, как будут измеряться значения. 
Из этого можно сделать вывод, что чем быстрее меняется сигнал с датчика, тем чаще его нужно опрашивать. Но вообще всё зависит от целей, который должна выполнять программа и проект в целом. На этом в принципе и строится обработка сигналов.
Фильтры
Цифровые (программные) фильтры позволяют отфильтровать различные шумы. В следующих примерах будут показаны некоторые популярные фильтры. Все примеры оформлены как фильтрующая функция, которой в качестве параметра передаётся новое значение, и функция возвращает фильтрованную величину. Некоторым функциям нужны дополнительные настройки, которые вынесены как переменные. Важно: практически каждый фильтр можно настроить лучше, чем показано на примерах с графиками. На примерах фильтр специально настроен не идеально, чтобы можно было оценить особенность работы алгоритма каждого из фильтров.
Среднее арифметическое
Однократная выборка
Среднее арифметическое вычисляется как сумма значений, делённая на их количество. Первый алгоритм именно так и работает: в цикле суммируем всё в какую-нибудь переменную, потом делим на количество измерений. Вуаля!
const int NUM_READ = 30; // количество усреднений для средних арифм. фильтров
// обычное среднее арифметическое для float
float midArifm() {
float sum = 0; // локальная переменная sum
for (int i = 0; i < NUM_READ; i++) // согласно количеству усреднений
sum += значение; // суммируем значения с любого датчика в переменную sum
return (sum / NUM_READ);
}
// обычное среднее арифметическое для int
int midArifm() {
long sum = 0; // локальная переменная sum
for (int i = 0; i < NUM_READ; i++) // согласно количеству усреднений
sum += значение; // суммируем значения с любого датчика в переменную sum
return ((float)sum / NUM_READ);
}
Особенности использования
- Отлично усредняет шум любого характера и величины
- Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
- “Сила” фильтра настраивается размером выборки (NUM_READS)
- Делает несколько измерений за один раз, что может приводить к большим затратам времени!
- Рекомендуется использовать там, где время одного измерения ничтожно мало, или измерения в принципе делаются редко
Растянутая выборка
Отличается от предыдущего тем, что суммирует несколько измерений, и только после этого выдаёт результат. Между расчётами выдаёт предыдущий результат:
const int NUM_READ = 10; // количество усреднений для средних арифм. фильтров
// растянутое среднее арифметическое
float midArifm2(float newVal) {
static byte counter = 0; // счётчик
static float prevResult = 0; // хранит предыдущее готовое значение
static float sum = 0; // сумма
sum += newVal; // суммируем новое значение
counter++; // счётчик++
if (counter == NUM_READ) { // достигли кол-ва измерений
prevResult = sum / NUM_READ; // считаем среднее
sum = 0; // обнуляем сумму
counter = 0; // сброс счётчика
}
return prevResult;
}
Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.
Особенности использования
- Отлично усредняет шум любого характера и величины
- “Сила” фильтра настраивается размером выборки (NUM_READS)
- Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
- Делает только одно измерение за раз, не блокирует код на длительный период
- Рекомендуется использовать там, где сам сигнал изменяется медленно, потому что за счёт растянутой по времени выборки сигнал может успеть измениться
Бегущее среднее арифметическое
Данный алгоритм работает по принципу буфера, в котором хранятся несколько последних измерений для усреднения. При каждом вызове фильтра буфер сдвигается, в него добавляется новое значение и убирается самое старое, далее буфер усредняется по среднему арифметическому. Есть два варианта исполнения: понятный и оптимальный:
const int NUM_READ = 10; // количество усреднений для средних арифм. фильтров
// бегущее среднее арифметическое
float runMiddleArifm(float newVal) { // принимает новое значение
static byte idx = 0; // индекс
static float valArray[NUM_READ]; // массив
valArray[idx] = newVal; // пишем каждый раз в новую ячейку
if (++idx >= NUM_READ) idx = 0; // перезаписывая самое старое значение
float average = 0; // обнуляем среднее
for (int i = 0; i < NUM_READ; i++) {
average += valArray[i]; // суммируем
}
return (float)average / NUM_READ; // возвращаем
}
// оптимальное бегущее среднее арифметическое
float runMiddleArifmOptim(float newVal) {
static int t = 0;
static float vals[NUM_READ];
static float average = 0;
if (++t >= NUM_READ) t = 0; // перемотка t
average -= vals[t]; // вычитаем старое
average += newVal; // прибавляем новое
vals[t] = newVal; // запоминаем в массив
return ((float)average / NUM_READ);
}
Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.
Особенности использования
- Усредняет последние N измерений, за счёт чего значение запаздывает. Нуждается в тонкой настройке частоты опроса и размера выборки
- Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
- “Сила” фильтра настраивается размером выборки (NUM_READS)
- Делает только одно измерение за раз, не блокирует код на длительный период
- Данный фильтр показываю чисто для ознакомления, в реальных проектах лучше использовать бегущее среднее. О нём ниже
Экспоненциальное бегущее среднее
Бегущее среднее (Running Average) – самый простой и эффективный фильтр значений, по эффекту аналогичен предыдущему, но гораздо оптимальнее в плане реализации фильтрованное += (новое - фильтрованное) * коэффициент:
float k = 0.1; // коэффициент фильтрации, 0.0-1.0
// бегущее среднее
float expRunningAverage(float newVal) {
static float filVal = 0;
filVal += (newVal - filVal) * k;
return filVal;
}
Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.
Особенности использования
- Самый лёгкий, быстрый и простой для вычисления алгоритм! В то же время очень эффективный
- “Сила” фильтра настраивается коэффициентом (0.0 – 1.0). Чем он меньше, тем плавнее фильтр
- Делает только одно измерение за раз, не блокирует код на длительный период
- Чем чаще измерения, тем лучше работает
- При маленьких значениях коэффициента работает очень плавно, что также можно использовать в своих целях
Вот так бегущее среднее справляется с равномерно растущим сигналом + случайные выбросы. Синий график – реальное значение, красный – фильтрованное с коэффициентом 0.1, зелёное – коэффициент 0.5. 
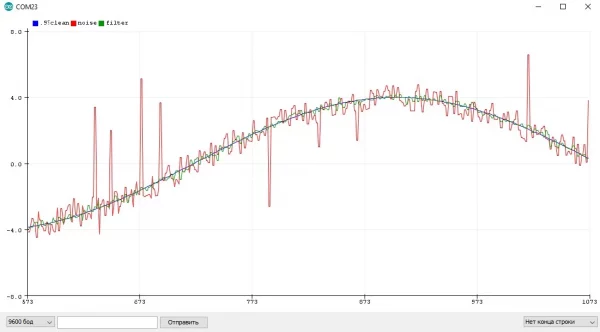
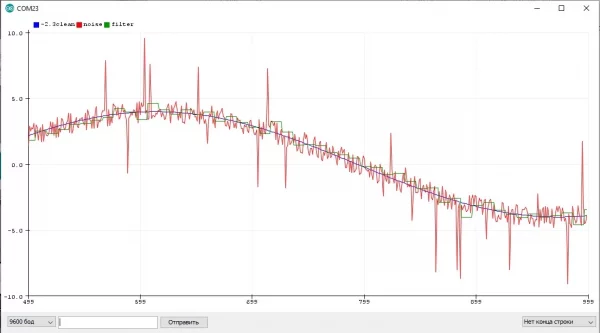
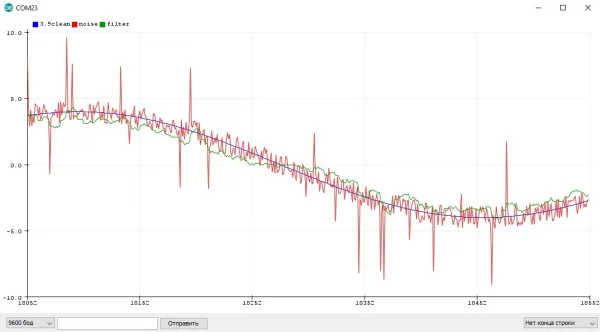
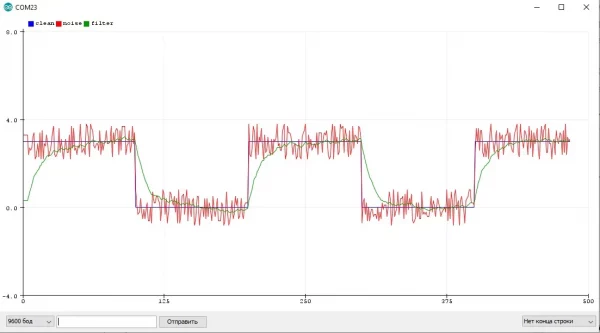
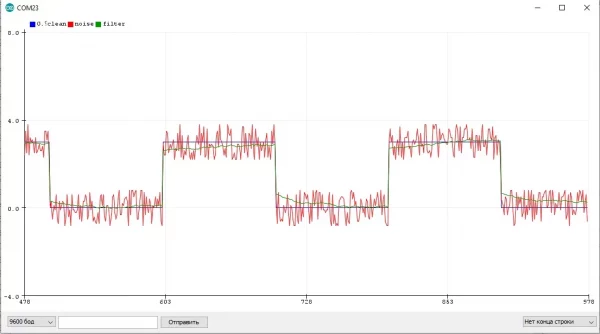
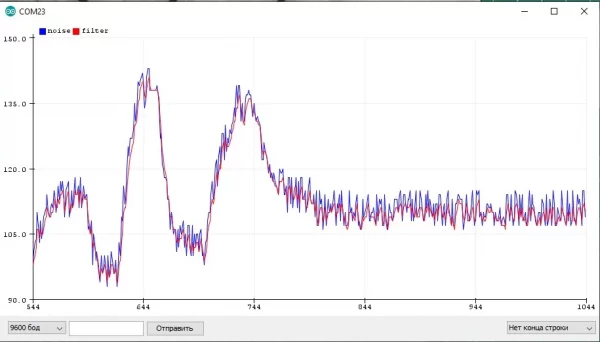
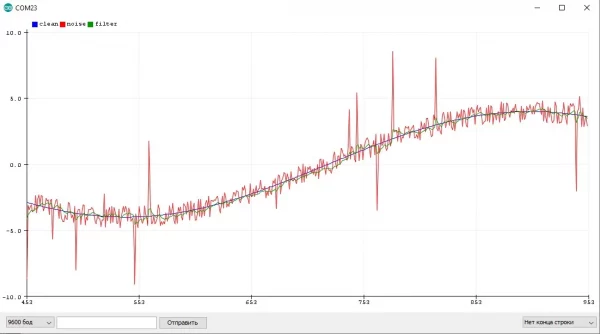
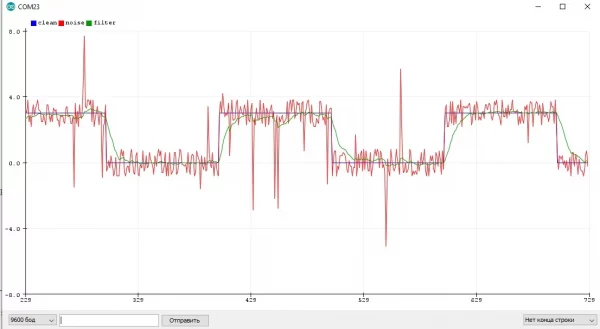
Пример с шумящим синусом
Пример с шумным квадратным сигналом, на котором видно запаздывание фильтра:
Адаптивный коэффициент
Чтобы бегущее среднее корректно работало с резко изменяющимися сигналами, коэффициент можно сделать адаптивным, чтобы он подстраивался под резкие изменения значения, например так: если фильтрованное значение “далеко” от реального – коэффициент резко увеличивается, позволяя быстро сократить “разрыв” между величинами. Если значение “близко” – коэффициент ставится маленьким, чтобы хорошо фильтровать шум:
// бегущее среднее с адаптивным коэффициентом
float expRunningAverageAdaptive(float newVal) {
static float filVal = 0;
float k;
// резкость фильтра зависит от модуля разности значений
if (abs(newVal - filVal) > 1.5) k = 0.9;
else k = 0.03;
filVal += (newVal - filVal) * k;
return filVal;
}
Таким образом даже простейший фильтр можно “программировать” и делать более умным. В этом и заключается прелесть программирования! 
Простой пример
Покажу отдельный простой пример реальной работы фильтра бегущее среднее, как самого часто используемого. Остальные фильтры – по аналогии. Фильтровать будем сигнал с аналогового пина А0:
void setup() {
Serial.begin(9600);
Serial.println("raw , filter");
}
float filtVal = 0;
void loop() {
int newVal = analogRead(0);
filtVal += (newVal - filtVal) * 0.1;
Serial.print(newVal);
Serial.print(',');
Serial.println(filtVal);
delay(10);
}
Код выводит в порт реальное и фильтрованное значение. Можно подключить к А0 потенциометр и покрутить его, наблюдая за графиком.
Целочисленная реализация
Для экономии ресурсов МК (поддержка дробных чисел требует пару килобайт Flash) можно отказаться от float и сделать фильтр целочисленным, для этого все переменные будут целого типа, а вместо умножения на дробный коэффициент будем делить на целое число, например fil += (val - fil) / 10 – получим фильтр с коэффициентом 0.1. Если вы читали урок по оптимизации кода, то знаете, что умножение на float быстрее деления на целое число! Не беда, всегда можно заменить деление сдвигом. Например фильтр с коэффициентом 1/16 можно записать так: fil += (val - fil) >> 4. Оптимизировать получится коэффициенты, кратные “степени двойки”, то есть 1/2, 1/4, 1/8 и так далее.
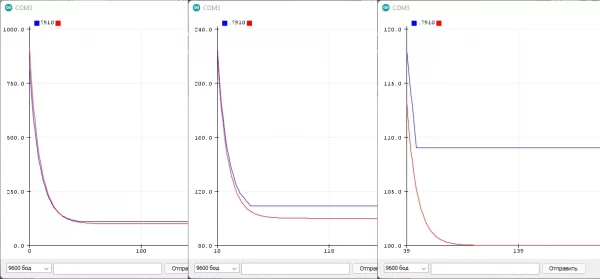
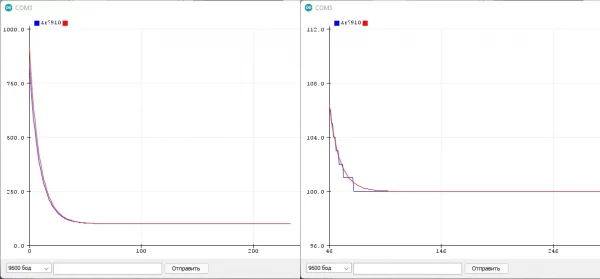
Но есть один неприятный момент: в реализации с float у нас в распоряжении огромная точность вычислений и максимальная плавность фильтра, фильтрованное значение со временем полностью совпадёт с текущим. В целочисленной же реализации точность будет ограничена коэффициентом: если разность в скобках (фильтрованное – текущее) будет меньше делителя – переменная фильтра не изменится, так как к ней будет прибавляться 0! Простой пример: float и целочисленный фильтры “фильтруют” величину от значения 1000 к значению 100 с коэффициентом 0.1 (используем число 10 для наглядности):
fu += (val - fu) / 10; ff += (val - ff) * 0.1;
Посмотрим графики:
Где синий график – целочисленный фильтр, красный – float. Из графика видно, что фильтры работают +- одинаково, но вот целочисленный резко остановился на значении 109, как и ожидалось: в уравнении фильтра получается (100 – 109) / 10, что даёт 0 и переменная фильтра больше не меняется. Таким образом точность фильтра определяется делителем коэффициента. Поэтому при использовании целочисленной реализации нужно подумать о двух вещах:
- Либо порядок фильтруемых величин у нас такой, что точность +- делитель не критична
- Либо искусственно повышаем разрядность фильтра следующим образом: переменная фильтра хранит увеличенное значение, и текущее значение мы для вычислений тоже домножаем, а при получении результата – делим, например:
fu += (val * 16 - fu) / 10; Serial.print(fu / 16);
Или на сдвигах:
fu += ((val << 4) - fu) / 10; Serial.print(fu >> 4);
Таким образом переменная фильтра хранит наше число с 16 кратной точностью, что позволяет в 16 раз увеличить плавность фильтра на критическом участке.
Не забываем, что сдвиг может переполнить два байта и вычисление будет неправильным. Можно заранее прикинуть и подбирать коэффициенты так, чтобы не превышать 2 байта в вычислениях, либо приводить к uint32_t.
fu += (uint32_t)(((uint32_t)val << 4) - fu) >> 5; Serial.print(fu >> 4);
Ошибка фильтра
На первой картинке с графиками в этой главе видно, что фильтрованное значение не достигает реального – отстаёт на величину фильтра. Для решения этой проблемы можно использовать следующую конструкцию, которая хранит “ошибку” фильтра и потом учитывает её:
// глобальные или статические int filt = 0; int err = 0; // сам фильтр int sum = (val - filt) + err; filt += sum / k; err = sum % k;
Модификацию с ошибкой можно применить и целочисленным вариантам из следующей главы. Также можно слегка оптимизировать этот код, заменив взятие остатка от деления умножением:
// глобальные или статические int filt = 0; int err = 0; // сам фильтр int sum = (val - filt) + err; int div = sum / k; filt += div; err = sum - div * k;
Ещё целочисленные варианты
На сайте easyelectronics есть отличная статья по целочисленным реализациям, давайте коротко их рассмотрим.
Вариант 1
Фильтр не имеет настроек, состоит из сложения и двух сдвигов, выполняется моментально. По сути это среднее арифметическое, или же рассмотренный выше фильтр с коэффициентом 1/2.
filt = (filt >> 1) + (signal >> 1);
Вариант 2
filt = (A * filt + B * signal) >> k;
Коэффициенты у этого фильтра выбираются следующим образом:
- k = 1, 2, 3…
- A + B = 2^k
- Чем больше А, тем плавнее фильтр (отношение A/B)
- Чем больше k, тем более плавным можно сделать фильтр. Но больше 5 уже нет смысла, т.к. A=31, B=1 уже очень плавно, а при увеличении может переполниться int и придётся использовать 32-х битные типы данных.
- Результат умножения не должен выходить за int, иначе придётся преобразовывать к long
- Более подробно о выборе коэффициентов читайте в статье, ссылка выше
- Особенность: если “ошибка” сигнала (signal – filter) меньше 2^k – фильтрованное значение меняться не будет. Для повышения “разрешения” фильтра можно домножить (или сдвинуть) переменную фильтра, то есть фильтровать в бОльших величинах
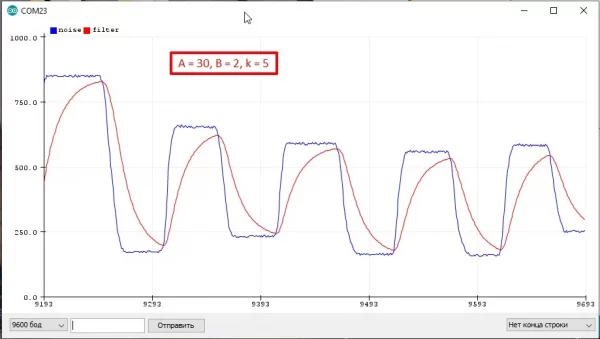
Например k = 4, значит A+B = 16. Хотим плавный фильтр, принимаем A=14, B=16: filt = (14 * filt + 2 * signal) >> 4;
Вариант 3
Третий алгоритм вытекает из второго: коэффициент B принимаем равным 1 и экономим одно умножение: filt = (A * filt + signal) >> k;
Тогда коэффициенты выбираются так:
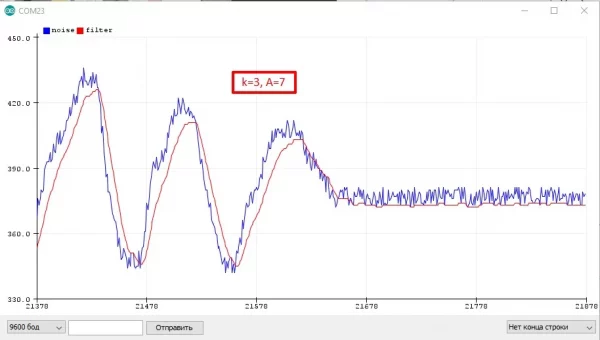
- k = 1, 2, 3…
- A = (2^k) – 1
- [k=2 A=3], [k=3 A=7], [k=4 A=15], [k=5 A=31]…
- Чем больше k, тем плавнее фильтр
Медианный фильтр
Медианный фильтр тоже находит среднее значение, но не усредняя, а выбирая его из представленных. Алгоритм для медианы 3-го порядка (выбор из трёх значений) выглядит так:
int middle;
if ((a <= b) && (a <= c)) middle = (b <= c) ? b : c;
else {
if ((b <= a) && (b <= c)) middle = (a <= c) ? a : c;
else middle = (a <= b) ? a : b;
}
// тут middle - ваша медиана
Мой постоянный читатель Андрей Степанов предложил сокращённую версию этого алгоритма, которая занимает одну строку кода и выполняется чуть быстрее за счёт меньшего количества сравнений:
middle = (a < b) ? ((b < c) ? b : ((c < a) ? a : c)) : ((a < c) ? a : ((c < b) ? b : c));
Можно ещё визуально сократить за счёт использования функций min() и max():
middle = (max(a,b) == max(b, c)) ? max(a, c) : max(b, min(a, c));
Для удобства использования можно сделать функцию, которая будет хранить в себе буфер на последние три значения и автоматически добавлять в него новые:
// медиана на 3 значения со своим буфером
int median(int newVal) {
static int buf[3];
static byte count = 0;
buf[count] = newVal;
if (++count >= 3) count = 0;
return (max(buf[0], buf[1]) == max(buf[1], buf[2])) ? max(buf[0], buf[2]) : max(buf[1], min(buf[0], buf[2]));
}
Большое преимущество медианного фильтра заключается в том, что он ничего не вычислят, а просто сравнивает числа. Это делает его быстрее фильтров других типов!
Медиана для большего окна значений описывается весьма внушительным алгоритмом, но я предлагаю пару более оптимальных вариантов:
Особенности использования- Медиана отлично фильтрует резкие изменения значения
- Делает только одно измерение за раз, не блокирует код на длительный период
- Алгоритм “больше трёх” весьма громоздкий
- Запаздывает на половину размерности фильтра
Простой “Калман”
Данный алгоритм я нашёл на просторах Интернета, источник потерял. В фильтре настраивается разброс измерения (ожидаемый шум измерения), разброс оценки (подстраивается сам в процессе работы фильтра, можно поставить таким же как разброс измерения), скорость изменения значений (0.001-1, варьировать самому).
float _err_measure = 0.8; // примерный шум измерений
float _q = 0.1; // скорость изменения значений 0.001-1, варьировать самому
float simpleKalman(float newVal) {
float _kalman_gain, _current_estimate;
static float _err_estimate = _err_measure;
static float _last_estimate;
_kalman_gain = (float)_err_estimate / (_err_estimate + _err_measure);
_current_estimate = _last_estimate + (float)_kalman_gain * (newVal - _last_estimate);
_err_estimate = (1.0 - _kalman_gain) * _err_estimate + fabs(_last_estimate - _current_estimate) * _q;
_last_estimate = _current_estimate;
return _current_estimate;
}
Особенности использования
- Хорошо фильтрует и постоянный шум, и резкие выбросы
- Делает только одно измерение за раз, не блокирует код на длительный период
- Слегка запаздывает, как бегущее среднее
- Подстраивается в процессе работы
- Чем чаще измерения, тем лучше работает
- Алгоритм весьма тяжёлый, вычисление длится ~90 мкс при системной частоте 16 МГц
Альфа-Бета фильтр
AB фильтр тоже является одним из видов фильтра Калмана, подробнее можно почитать можно на Википедии.
// период дискретизации (измерений), process variation, noise variation
float dt = 0.02;
float sigma_process = 3.0;
float sigma_noise = 0.7;
float ABfilter(float newVal) {
static float xk_1, vk_1, a, b;
static float xk, vk, rk;
static float xm;
float lambda = (float)sigma_process * dt * dt / sigma_noise;
float r = (4 + lambda - (float)sqrt(8 * lambda + lambda * lambda)) / 4;
a = (float)1 - r * r;
b = (float)2 * (2 - a) - 4 * (float)sqrt(1 - a);
xm = newVal;
xk = xk_1 + ((float) vk_1 * dt );
vk = vk_1;
rk = xm - xk;
xk += (float)a * rk;
vk += (float)( b * rk ) / dt;
xk_1 = xk;
vk_1 = vk;
return xk_1;
}
Особенности использования
- Хороший фильтр, если правильно настроить
- Но очень тяжёлый!
Метод наименьших квадратов
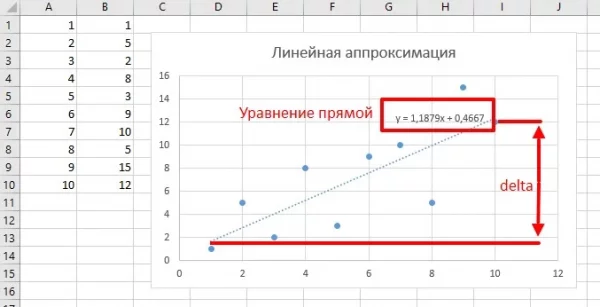
Следующий фильтр позволяет наблюдать за шумным процессом и предсказывать его поведение, называется он метод наименьших квадратов, теорию читаем тут. Чисто графическое объяснение здесь такое: у нас есть набор данных в виде несколько точек. Мы видим, что общее направление идёт на увеличение, но шум не позволяет сделать точный вывод или прогноз. Предположим, что существует линия, сумма квадратов расстояний от каждой точки до которой – минимальна. Такая линия наиболее точно будет показывать реальное изменение среди шумного значения. В какой то статье я нашел алгоритм, который позволяет найти параметры этой линии, опять же портировал на с++ и готов вам показать. Этот алгоритм выдает параметры прямой линии, которая равноудалена от всех точек.
float a, b, delta; // переменные, которые получат значения после вызова minQuad
void minQuad(int *x_array, int *y_array, int arrSize) {
int32_t sumX = 0, sumY = 0, sumX2 = 0, sumXY = 0;
arrSize /= sizeof(int);
for (int i = 0; i < arrSize; i++) { // для всех элементов массива
sumX += x_array[i];
sumY += (long)y_array[i];
sumX2 += x_array[i] * x_array[i];
sumXY += (long)y_array[i] * x_array[i];
}
a = (long)arrSize * sumXY; // расчёт коэффициента наклона прямой
a = a - (long)sumX * sumY;
a = (float)a / (arrSize * sumX2 - sumX * sumX);
b = (float)(sumY - (float)a * sumX) / arrSize;
delta = a * (x_array[arrSize-1] - x_array[0]); // расчёт изменения
}
Особенности использования
- В моей реализации принимает два массива и рассчитывает параметры линии, равноудалённой от всех точек
Какой фильтр выбрать?
Выбор фильтра зависит от типа сигнала и ограничений по времени фильтрации. Среднее арифметическое – хорошо подходит, если фильтрации производятся редко и время одного измерения значения мало. Для большинства ситуаций подходит бегущее среднее, он довольно быстрый и даёт хороший результат на правильной настройке. Медианный фильтр 3-го порядка тоже очень быстрый, но он может только отсеить выбросы, сам сигнал он не сгладит. Медиана большего порядка является довольно более громоздким и долгим алгоритмом, но работает уже лучше. Очень хорошо работает медиана 3 порядка + бегущее среднее, получается сглаженный сигнал с отфильтрованными выбросами (сначала фильтровать медианой, потом бегущим). AB фильтр и фильтр Калмана – отличные фильтры, справляются с шумным сигналом не хуже связки медиана + бегущее среднее, но нуждаются в тонкой настройке, также они довольно громоздкие с точки зрения кода. Линейная аппроксимация – инструмент специального назначения, позволяющий буквально предсказывать поведение значения за период – ведь мы получаем уравнение прямой. Если нужно максимальное быстродействие – работаем только с целыми числами и используем целочисленные фильтры.
Библиотека GyverFilters
Библиотека содержит все описанные выше фильтры в виде удобного инструмента для Arduino. Документацию и примеры к библиотеке можно посмотреть здесь.
- GFilterRA – компактная альтернатива фильтра экспоненциальное бегущее среднее (Running Average)
- GMedian3 – быстрый медианный фильтр 3-го порядка (отсекает выбросы)
- GMedian – медианный фильтр N-го порядка. Порядок настраивается в GyverFilters.h – MEDIAN_FILTER_SIZE
- GABfilter – альфа-бета фильтр (разновидность Калмана для одномерного случая)
- GKalman – упрощённый Калман для одномерного случая (на мой взгляд лучший из фильтров)
- GLinear – линейная аппроксимация методом наименьших квадратов для двух массивов
Видео
Полезные страницы
- Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
- Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
- Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
- Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
- Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
- Поддержать автора за работу над уроками
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])