ПИД регулятор

ПИД регулятор - один из самых распространенных автоматических регуляторов. Он настолько универсален, что применяется практически везде, где нужно автоматическое управление. Например температурой: печи, холодильники, инкубаторы, паяльники, сопло и стол 3D принтера, ИК паяльные станции и прочее. Поддержание частоты оборотов мотора, например для станков. Всевозможные балансирующие штуки, гироскутеры, сигвеи, левитирующие магнитные платформы, и конечно же квадрокоптеры и самолёты с автопилотом. Всё это - ПИД регулятор.

Почему именно ПИД? Существуют и другие регуляторы, превосходящие ПИД по адаптивности к управляемой системе и стабильности, например линейно квадратичный. Но синтезировать такой регулятор очень сложно, а настройка ПИД регулятора дело хоть и неприятное, но фактически очень простое и под силу любому, а сам регулятор занимает буквально 5 строк кода с очень простыми вычислениями.

Система управления #

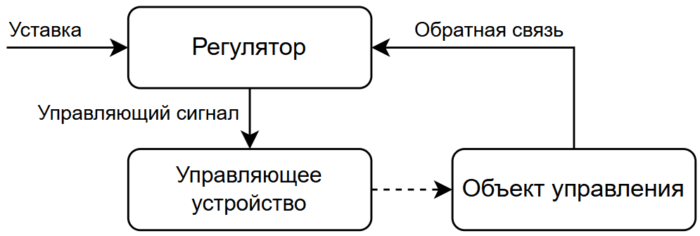
Прежде чем переходить непосредственно к ПИДу, очень важно понять и запомнить несколько базовых понятий, из которых состоит автоматическая система. В первую очередь это регулятор, который всем заправляет, в рамках этих уроков – математический алгоритм или часть программы, которая выполняется процессором.

Объект управления – это устройство, которым мы управляем, например печка или мотор. Для этого у нас есть управляющее устройство, например диммируемый тен или драйвер мотора. Управляющее устройство получает от регулятора управляющий сигнал, то есть конкретное число. Это может быть заполнение шим сигнала, от 0 до 255, а может быть угол поворота сервомашинки от 0 до 180 - регулятору без разницы чем управлять. В объекте управления стоит датчик, с которого регулятор получает величину, которой он по сути и управляет. Это - обратная связь, которая и даёт возможность системе точно поддержать заданное значение. В случае с печкой это температура, а с мотором – частота оборотов. Ну и наконец регулятор получает уставку (установку, настройку, заданное значение), то есть число, к которому он должен привести текущее значение с датчика. Уставка может быть фиксированной или задаваться каким угодно образом: крутилкой, ползунком, энкодером, кнопками - регулятору это неважно, для него это просто число.

Задача регулятора состоит в том, чтобы сравнивать текущее значение (обратная связь) с заданным (уставка) и выдавать управляющий сигнал на управляющее устройство. Ошибка регулирования - буквально разность уставки и обратной связи, на которую ориентируется регулятор. В программе это будет выглядеть условно так: регулятор получил значение с датчика, нашёл разницу с уставкой, произвёл вычисления и выдал управляющий сигнал. Если это ШИМ – мы его подаём через функцию генерации ШИМ, если угол для привода - отправляем на привод.

В программной (дискретной) реализации регулятор должен делать расчёты и применять управляющий сигнал через равные промежутки времени, то есть с равным периодом или частотой. Эта частота называется частотой дискретизации системы, а период обозначается как dt, прямо как период интегрирования. По сути это время в секундах, которое прошло с прошлого расчёта.

Под капотом у ПИД регулятора #

ПИД регулятор состоит из трёх составляющих: пропорциональной P (proportional), интегрирующей I (integral) и дифференциирующей D (derivative) и формируется просто как сумма трёх значений, умноженных каждая на свой коэффициент. Эта сумма после вычислений становится управляющим сигналом, который подаётся на управляющее устройство. Обозначим его как output:

output = P * Kp + I * Ki + D * Kd;

Где Kp, Ki и Kd это коэффициенты, которые нужно настроить для работы ПИДа. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы и её диапазона значений входа и выхода.

Тут есть ещё один момент: любой коэффициент может быть равен нулю, в таком случае обнуляется вся его компонента. То есть регулятор можно превратить в П, ПИ, ПД и прочие сочетания. Разные системы требуют разного подхода, именно поэтому ПИД регулятор такой универсальный.

В дальнейшем будем пользоваться следующими именами переменных:

• output - выход с регулятора (управляющий сигнал)
• setpoint - уставка (заданное значение)
• input - вход (значение с датчика)
• error - ошибка регулирования
• dt - период дискретизации

error = setpoint - input;

P составляющая #

Пропорциональная составляющая представляет собой текущее значение ошибки:

P = error;

Получается чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Коэффициент Kp тут играет роль усиления ошибки.

Если система пришла к заданной величине, то ошибка станет равной нулю - и управляющий сигнал тоже! Другими словами, П-регулятор никогда не сможет привести к заданному значению - всегда будет некая ошибка. П составляющая является основной в ПИД регуляторе и так сказать тянет самую большую лямку, регулятор может неплохо работать только лишь на ней одной.

I составляющая #

Интегральная составляющая суммирует в саму себя ошибку, умноженную на период дискретизации системы (время, прошедшее с предыдущего расчёта) - фактически берёт интеграл от ошибки по времени:

I = I + error * dt;

Здесь I - интегральная сумма накопившихся ошибок. Её нужно хранить между вызовами расчёта.

В самом регуляторе это ещё умножается на коэффициент Ki, которым и настраивается вклад данной составляющей в процесс. В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с минимальной ошибкой.

D составляющая #

Дифференциальная составляющая представляет собой разность текущей и предыдущей ошибок, поделенную на dt – это производная от ошибки по времени:

D = (error - prevError) / dt;
prevError = error;

Здесь prevError - предыдущая ошибка, которая нужна для расчёта производной. Её тоже нужно хранить между вызовами расчёта.

Фактически D составляющая реагирует на изменение сигнала с датчика и чем сильнее происходит это изменение, тем большее значение прибавляется к общей сумме. Иными словами, D позволяет компенсировать резкие изменения в системе и при правильной настройке предотвратить сильное перерегулирование и уменьшить раскачку, т.е. тормозит систему и уменьшает управляющий сигнал. Коэффициент Kd позволяет настроить вес данной компенсации. D составляющая в первую очередь нужна для быстрых систем, то есть для систем с резкими изменениями, таким как квадрокоптер или шпиндель станка под переменной нагрузкой.

Всё вместе #

Соединим всё вышесказанное в виде псевдокода:

error = setpoint - input;
I = I + error * dt;
D = (error - prevError) / dt;
prevError = error;
output = error * Kp + I * Ki + D * Kd;

Это и есть классический дискретный ПИД регулятор.

Реализация на Arduino/C #

Рассмотрим реализацию ПИД регулятора на Arduino для наглядности в виде набора переменных и функции для расчёта. Потом это можно очень просто обернуть например в класс:

float Kp, Ki, Kd;
float integral, pError;

float computePID(float setpoint, float input, float dt) {
    float error = setpoint - input;
    float derivative = (error - pError) / dt;
    pError = error;
    integral += error * dt;
    return error * Kp + integral * Ki + derivative * Kd;
}

Как использовать:

• Задать коэффициенты
• Вызывать функцию с некоторым периодом, этот период тоже передать в функцию
• Результат отправлять на управляющее устройство

Например:

void setup() {
    Kp = 10;
    Ki = 5;
    Kd = 1;
}

void loop() {
    float out = computePID(уставка, сигнал_с_датчика, 0.01);
    analogWrite(пин, out);
    delay(10);
    // 10 мс это 0.01 с
}

Настройка регулятора #

Для настройки регулятора нужно варьировать коэффициенты:

• При увеличении Kp увеличивается скорость выхода на установленное значение, увеличивается управляющий сигнал. Чисто математически система не может прийти ровно к заданному значению, так как при приближении к установке П составляющая пропорционально уменьшается. При дальнейшем увеличении Kp реальная система теряет устойчивость и начинаются колебания
• При увеличении Ki растёт скорость компенсации накопившейся ошибки, что позволяет вывести систему точно к заданному значению с течением времени. Если система медленная, а Ki слишком большой - интегральная сумма сильно вырастет и произойдёт перерегулирование, которое может иметь характер незатухающих колебаний с большим периодом. Поэтому интегральную сумму в алгоритме регулятора часто ограничивают, чтобы она не могла увеличиваться и уменьшаться до бесконечности
• При увеличении Kd растёт стабильность системы, она не даёт системе меняться слишком быстро. В то же время Kd может сам стать причиной неадекватного поведения системы и постоянных скачков управляющего сигнала, если значение с датчика шумит. На каждое резкое изменение сигнала с датчика Д составляющая будет реагировать изменением управляющего сигнала, поэтому сигнал с датчика нужно фильтровать

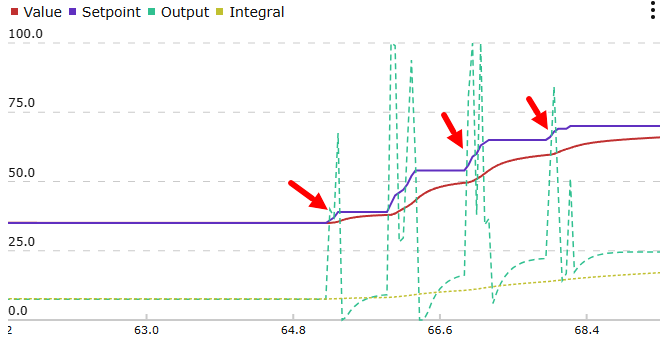
Вот так выглядит процесс стабилизации при изменении коэффициентов:

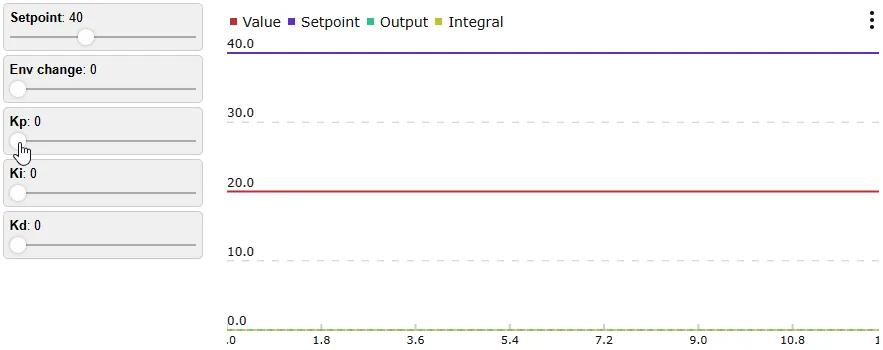
Симуляция нагрева, регулятор управляет нагревателем, выходной сигнал ограничен 0-100

Метод Циглера-Никольса #

Начальные коэффициенты для подбора можно получить по следующему алгоритму: сначала выставляем все коэффициенты в 0. Плавно увеличиваем Kp до появления незатухающих колебаний. Значение Kp, при котором они появились, запишем и обозначим как Kp1. Далее замеряем период колебаний системы в секундах - T. Итоговые коэффициенты получим как:

Kp = 0.6 * Kp1;
Ki = Kp / T * 2 * dt;
Kd = Kp * T / 8 / dt;

Например, незатухающие колебания появились при Kp = 20, период колебаний составил 3 секунды. Период dt в системе был например 50 мс (0.05 с). Считаем:

Kp: 0.6 * 20 = 12
Ki: 12 / 3 * 2 * 0.05 = 0.4
Kd: 12 * 2 / 8 / 0.05 = 60

На полученных коэффициентах должны более-менее работать большинство систем.

Модификации алгоритма #

D по входу #

В классическом PID Д составляющая считается от ошибки, которая равна setpoint - input, поэтому при изменении уставки будет провоцировать резкие выбросы на выходе, что может быть неприемлемо для некоторых систем:

Если сигнал уставки шумит - этот шум усилится и станет выходом регулятора, что сделает систему неустойчивой и очень дёрганой. Решение проблемы - слегка пересмотреть уравнение:

(error) - (prevError) = (setpoint - input) - (setpoint - prevInput) = prevInput - input

То есть брать производную не по ошибке, а по входу. Такая модификация практически всегда используется в промышленных контроллерах и позволяет:

• Уменьшить чувствительность к скачкам уставки
• Уменьшить шум в дифференцирующем канале
• Повысить стабильность и надёжность системы

Д по ошибке (классическая) используется в теоретических моделях и симуляциях, а также в системах, где важна высокая скорость отклика на ошибку. Полная реализация D по входу:

float Kp, Ki, Kd;
float integral, pInput;

float computePID(float setpoint, float input, float dt) {
    float error = setpoint - input;
    float derivative = (pInput - input) / dt;
    pInput = input;
    integral += error * dt;
    return error * Kp + integral * Ki + derivative * Kd;
}

Результат - нет таких сильных выбросов на выходе:

Внесение Ki в интеграл #

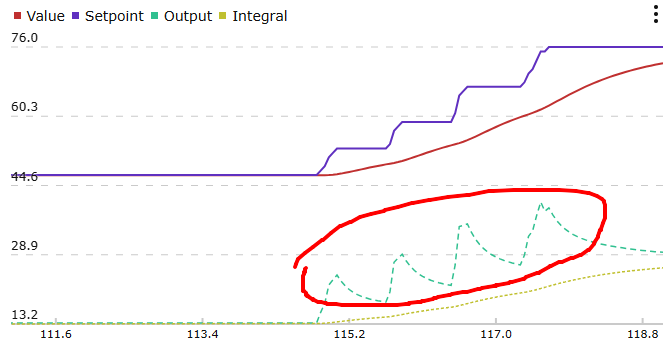
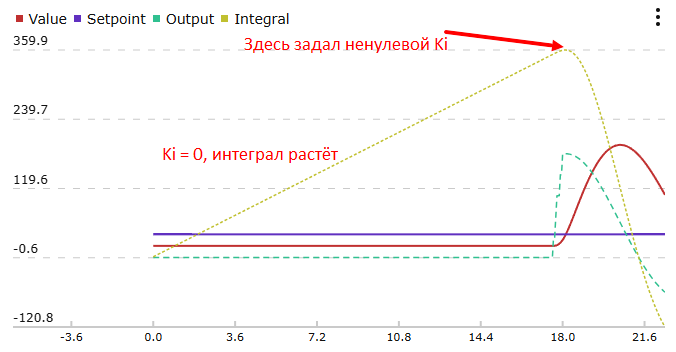
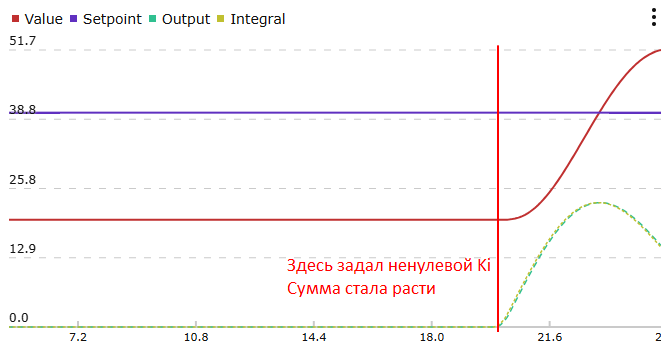
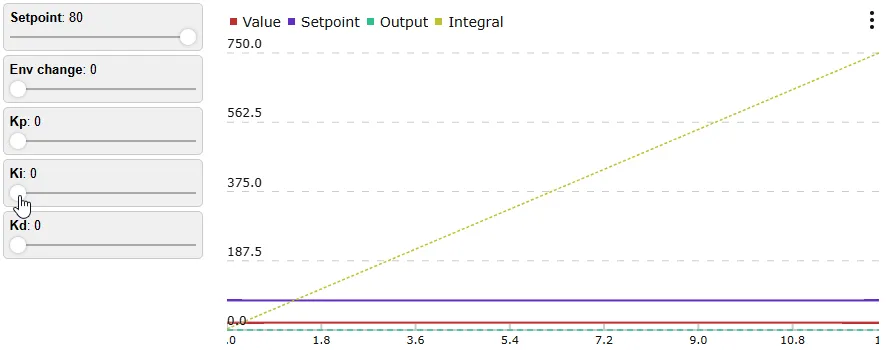
В классическом виде интеграл считается по ошибке, а затем умножается на Ki в выражении для выхода. Это приводит к тому, что интеграл живёт сам по себе, независимо от Ki. Например, мы запустили систему с нулевым Ki и увеличили его спустя некоторое время. За это время накопилась огромная интегральная ошибка, стабилизировать систему с ней будет непросто:

Решение - внести Ki в расчёт интеграла:

integral += error * Ki * dt;

Это никак не повлияет на саму математику алгоритма, но теперь интеграл будет зависеть от значения Ki и настраивать регулятор в реальном времени станет гораздо проще:

float Kp, Ki, Kd;
float integral, pError;

float computePID(float setpoint, float input, float dt) {
    float error = setpoint - input;
    float derivative = (error - pError) / dt;
    pError = error;
    integral += error * Ki * dt;
    return error * Kp + integral + derivative * Kd;
}

Однако теперь выход напрямую зависит от интеграла и, если например обнулить Ki в процессе работы регулятора, то сам накопившийся интеграл никуда не денется и будет всё ещё учитываться в расчёте выхода! Это нужно учитывать при разработке и настройке своего регулятора.

Обнуление интеграла #

В некоторых системах может хорошо работать обнуление интегральной суммы при достижении уставки, особенно когда параметры системы часто меняются и нужно избавиться от накопленных ошибок и реагировать быстрее:

error = setpoint - input;
I = I + error * dt;
if (input >= setpoint) I = 0;   // <- если выход регулятора увеличивает input
D = (error - prevError) / dt;
prevError = error;
output = error * Kp + I * Ki + D * Kd;

Насыщение #

Когда регулятор не может достигнуть уставки, интегральная сумма начинает бесконтрольно расти. Если внешние условия изменятся или например уменьшится уставка - интеграл останется очень большим и система отреагирует не сразу. Чтобы уменьшить время реакции в этой ситуации, нужно ограничить рост интегральной суммы. Это можно сделать даже так:

I = I + error * dt;
if (I > Imax) I = Imax;
else if (I < -Imax) I = -Imax;

Но каким выбрать Imax? Сложный вопрос.

Задачу можно решить по-другому - ограничивать рост интеграла, когда система входит в насыщение, т.е. когда выходное значение превышает некий лимит. Классический ПИД регулятор не знает лимита - он выдаёт такой выход, который получился при вычислении. На практике выход всегда имеет ограничение, например 0-255 для Arduino ШИМ или 0-180 градусов для сервопривода. Таким образом, если при расчёте получилось больше максимума или меньше минимума - говорят что выход в насыщении, это условие можно использовать для ограничения интеграла.

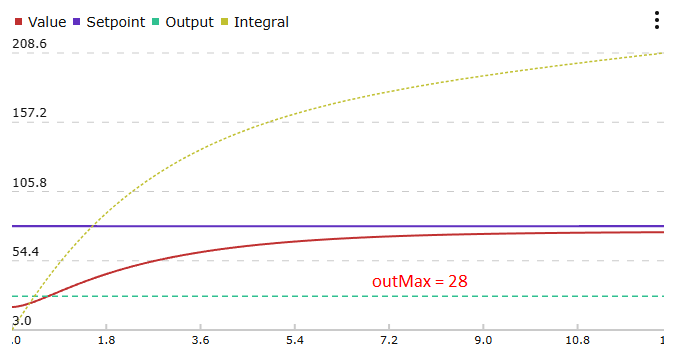
Выход в насыщении, интеграл растёт

Conditional Integration #

"Интегрирование по условию" - самый простой подход: не интегрируем I, если выход насыщен и интеграл собирается увеличиться по модулю:

float Kp, Ki, Kd;
float outMax = 0, outMin = 100;
float integral, pError;

float computePID(float setpoint, float input, float dt) {
    float error = setpoint - input;
    float derivative = (error - pError) / dt;
    pError = error;
    float output = error * Kp + integral * Ki + derivative * Kd;

    if (output >= outMax) {
        if (error > 0) return outMax;
    } else if (output <= outMin) {
        if (error < 0) return outMin;
    }

    integral += error * dt;
    return output;
}

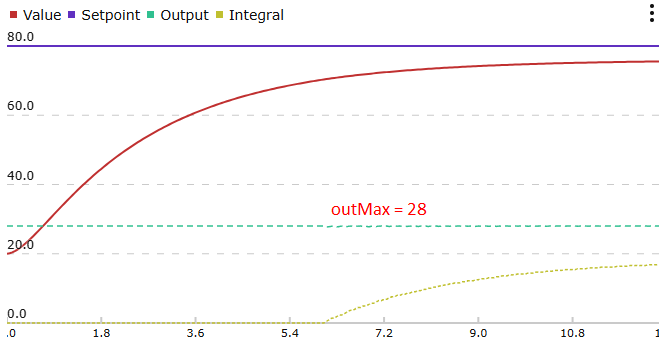
Интеграл не растёт из-за интегрирования по условию

Back Calculation #

Второй вариант более хитрый и с настройкой в виде дополнительного коэффициента, назовём его Kbc:

float Kp, Ki, Kd;
float Kbc;
float outMax = 0, outMin = 100;
float integral, pError;

float computePID(float setpoint, float input, float dt) {
    float error = setpoint - input;
    float derivative = (error - pError) / dt;
    pError = error;
    float output = error * Kp + integral * Ki + derivative * Kd;

    if (output >= outMax) {
        error += (outMax - output) * Kbc;
        output = outMax;
    } else if (output <= outMin) {
        error += (outMin - output) * Kbc;
        output = outMin;
    }

    integral += error * dt;
    return output;
}

Коэффициент Kbc подбирается под конкретную систему, начальным значением можно взять текущее Ki.

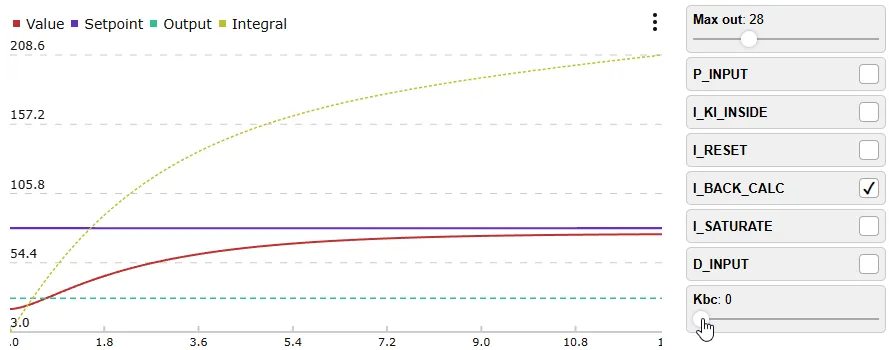
Влияние Kbc на интегральную сумму при насыщении

P по входу #

Ещё одна интересная модификация, которая используется на практике в промышленных контроллерах (Emerson, Siemens, Honeywell) и часто называется P on Measurement. Она полностью меняет привычную логику работы и поведение регулятора, хотя в уравнении меняется только P составляющая - вместо ошибки используется обратное значение входа:

error = setpoint - input;
I = I + error * dt;
D = (error - prevError) / dt;
prevError = error;
output = -input * Kp + I * Ki + D * Kd;

Если в классике P играет ключевую роль, а I компенсирует оставшуюся ошибку, то в таком регуляторе с "P по входу" основную роль играет уже I составляющая, а P наоборот - тормозит и стабилизирует систему. Преимущества перед "P по ошибке":

• Снижение резких скачков выхода при скачках уставки
• Меньшее перерегулирование
• Более плавный и устойчивый процесс

Алгоритм хорошо работает в медленных и инерционных системах, где недопустимо перерегулирование.

float Kp, Ki, Kd;
float integral, pError;

float computePID(float setpoint, float input, float dt) {
    float error = setpoint - input;
    float derivative = (error - pError) / dt;
    pError = error;
    integral += error * dt;
    return -input * Kp + integral * Ki + derivative * Kd;
}

Библиотеки #

• sTune - тюнер коэффициентов, несколько алгоритмов
• GyverPID - моя старая библиотека со встроенным тюнером коэффициентов
• uPID - моя новая универсальная библиотека, содержит все модификации из этого урока с настройкой в compile time

Видео #

Дополнительно #

Полезные страницы #

• Набор GyverKIT – наш большой стартовый набор Arduino, продаётся в России
• Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress
• Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])
• Поддержать автора за работу над уроками