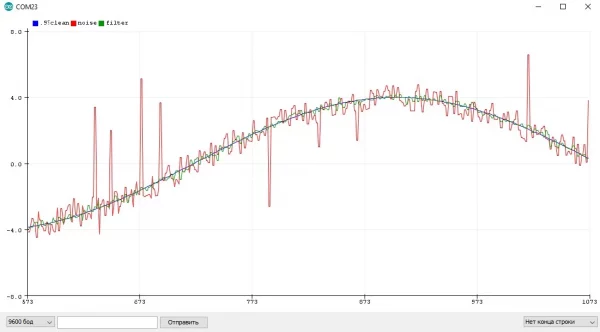
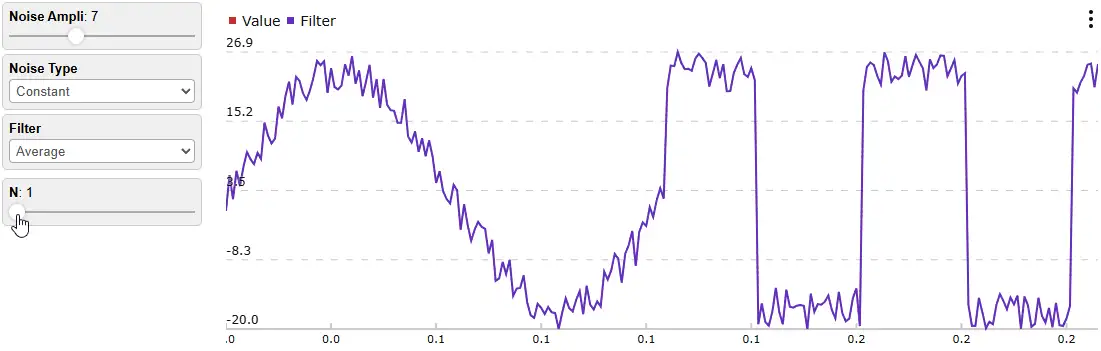
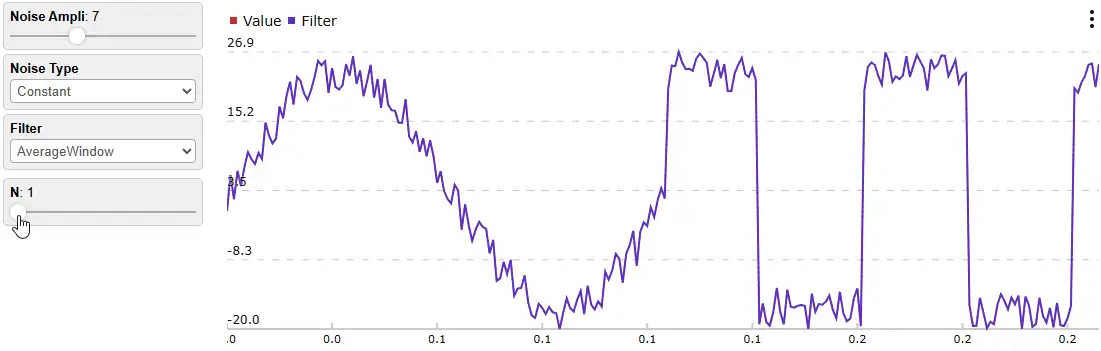
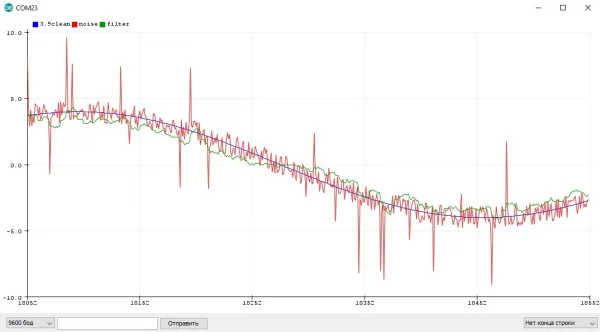
На практике данные почти с любого датчика редко бывают идеальными и стабильными, т.е. при неизменных внешних условиях каждое следующее значение с датчика может отличаться от предыдущего - это называется шумом измерения. В некоторых случаях шум в сигнале можно уменьшить аппаратно (улучшение качества питания, экранирование проводов), но это не всегда возможно - шумящий сигнал всё равно попадёт в программу. Здесь его можно уменьшить при помощи программных, или цифровых фильтров - фильтров, которые работают с числами.
Примечание: данный урок не объясняет подробно работу алгоритмов, т.к. теория по некоторым фильтрам содержит очень сложную математику и не уместится по объёму в несколько уроков подобного размера. Это - обзорная экскурсия по популярным фильтрам, особенностям и сценариям их использования и настройки, а также готовый код для добавления в программу, чаще всего в виде удобного компактного класса.
Измерения #
Тип шума #
Шум можно условно разделить на три типа:
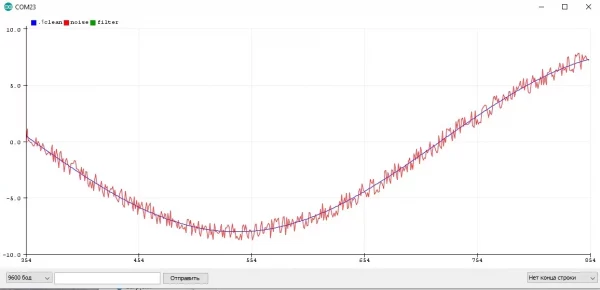
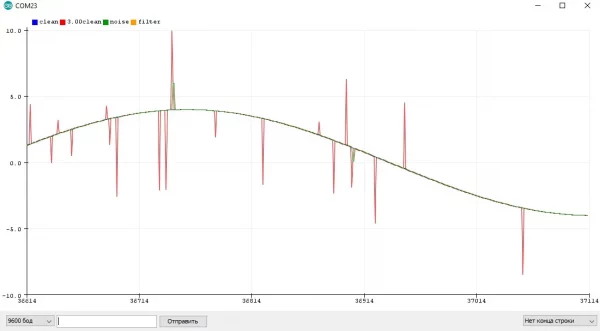
- Постоянный равномерный шум "вокруг" реального значения, такой сигнал выглядит как пилообразная линия. Чаще всего наблюдается в измерениях АЦП или датчиков на основе АЦП при наличии рядом постоянного источника помех или при питании АЦП от шумного импульсного источника питания. Также довольно часто АЦП имеет собственный шум в несколько единиц даже при идеальном питании. Это самый простой шум, его легко отфильтровать почти любым фильтром
- Импульсный случайный шум, который выглядит как единичный пик или серия пиков на графике. Такой шум может выдать датчик на основе АЦП при единичных электромагнитных помехах (от мотора или другой катушки), датчик расстояния при попадании мелкой "цели" в поле зрения, GPS при перебоях со связью, дребезг кнопки и так далее. Такой шум нуждается в отдельной ступени фильтрации
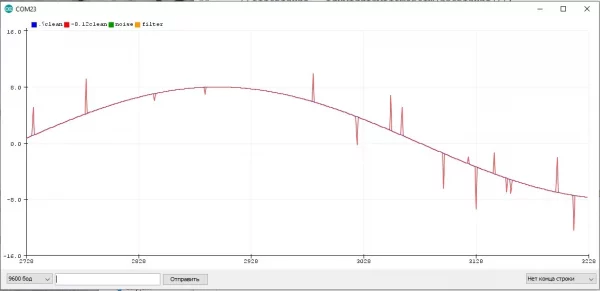
- Дрейф - показания с датчика безвозвратно "уходят" от реального значения, например тахо-датчик расстояния при проскальзывании колёс или полученные интегрированием гироскопа координаты. Это - самый сложный шум, для его устранения нужно обрабатывать данные с нескольких датчиков при помощи хитрых алгоритмов, например фильтра Калмана. В рамках данного урока такие "многомерные" системы и фильтры не рассматриваются, возможно позже им будет посвящён отдельный урок
Постоянный и импульсный шумы:
Параметры шума #
Некоторые описанные ниже фильтры будут требовать для аналитической настройки (не "на глаз") определённых параметров шума сигнала, в рамках этого урока хватает двух:
- Дисперсия (variance) - это среднее значение квадратов отклонений всех элементов от их среднего арифметического значения. Значение является квадратом и даже обозначается как "сигма в квадрате". Чем больше дисперсия, тем сильнее "разбросаны" данные, а если дисперсия равна нулю - значения одинаковы
- Стандартное отклонение или квадратичное отклонение (standard deviation, stddev) - квадратный корень из дисперсии, показывает среднюю величину отклонения от среднего значения
Идеальный шум #
У "идеального" шума эти параметры приблизительно равны:
- Дисперсия:
амплитуда / 12 - Стд. отклонение:
амплитуда * 0.29- правило "трёх сигм", амплитуда равна трём сигмам
Это может помочь при начальной настройке фильтра - нужно замерить амплитуду шума на участке, где сам сигнал стабилен, и получить нужную величину по формуле выше.
Калкулятор шума #
Прилагаю калькулятор параметров шума - нужно ввести в первое поле значения сигнала через запятую и нажать кнопку "Расчёт":
Измерение параметров #
Параметры шума можно замерить прямо "в железе" при помощи алгоритма Уэлфорда:
class WelfordStat {
public:
// добавить значение
void add(float value) {
++_n;
float delta = value - _mean;
_mean += delta / _n;
float delta2 = value - _mean;
_m2 += delta * delta2;
}
// среднее
float mean() const {
return _mean;
}
// дисперсия
float variance() const {
return (_n > 1) ? _m2 / (_n - 1) : 0;
}
// стандартное отклонение
float stddev() const {
return sqrt(variance());
}
private:
int _n = 0;
float _mean = 0;
float _m2 = 0;
};Для примера изучим стандартную функцию random():
WelfordStat st;
void loop() {
st.add(random(100));
Serial.print(st.mean());
Serial.print(',');
Serial.print(st.variance());
Serial.print(',');
Serial.print(st.stddev());
Serial.println();
// 47.92,870.12,29.50
delay(50);
}Частота измерений #
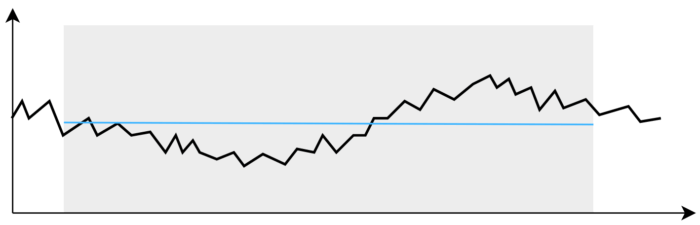
Давайте посмотрим, как измеряется сигнал в реальном устройстве. Естественно, это происходит не каждую итерацию loop, а с некоторой частотой, эта частота называется частотой дискретизации, т.е. сигнал превращается в цифровой, дискретный. Обратное значение частоте - период, т.е. буквально время между двумя измерениями: period = 1 / freq [сек = 1 / Гц].
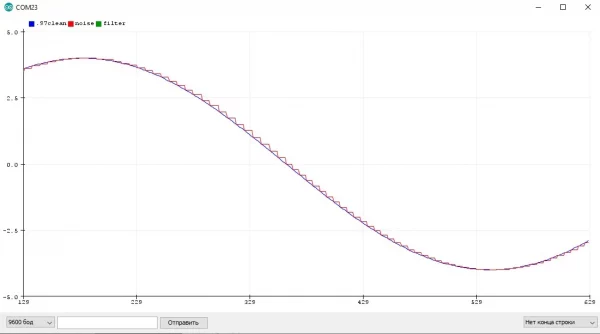
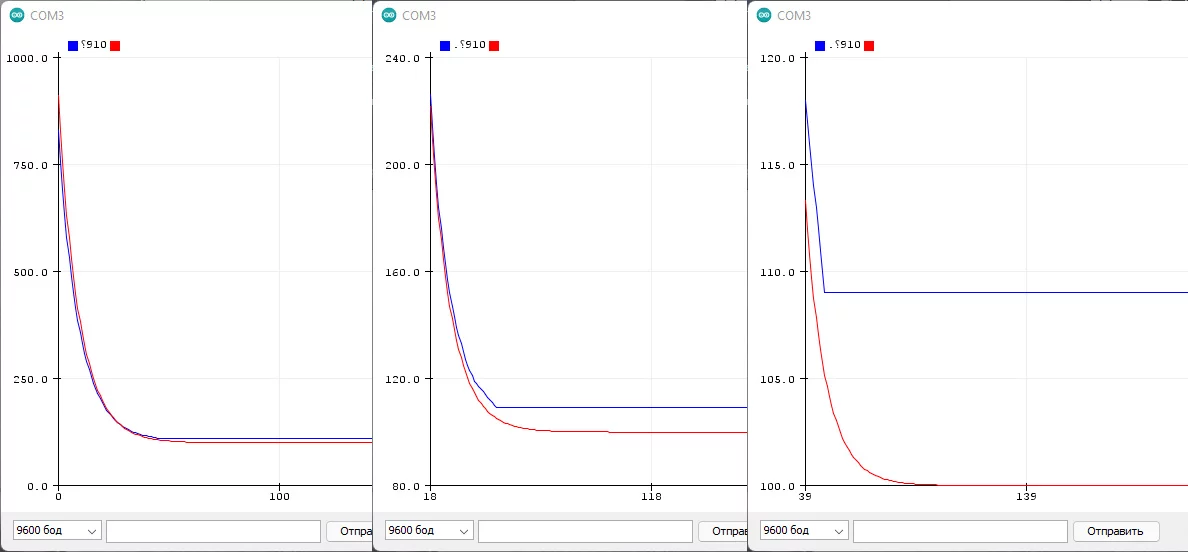
Представим, что синий график отражает реальный "непрерывный" процесс, а красный - измеренное контроллером значение:
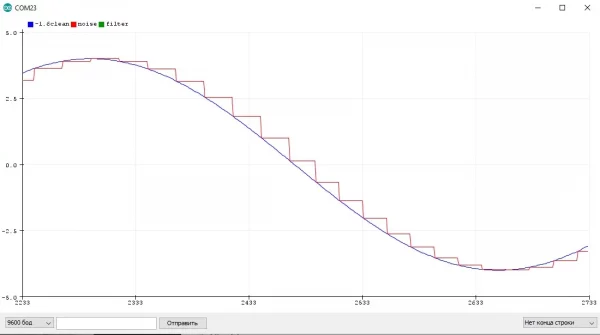
Очевидно, что между измерениями значение не меняется и остаётся постоянным. Увеличим период:
Из этого можно сделать вывод, что чем быстрее процесс, тем чаще нужно опрашивать датчик, особенно если система должна сразу реагировать на изменение. А если сигнал шумит, то чем чаще мы будем опрашивать датчик, тем эффективнее сможет работать фильтр и тем ближе фильтрованный сигнал будет к реальному. Но есть и разумные пределы.
Для фильтра #
Частота опроса сигнала для фильтра - очень важный параметр. Если она будет слишком низкой - фильтр может пропустить быстрое изменение сигнала, отстать от него. Если слишком высокой - фильтр может сосредоточиться на фильтрации мелких высокочастотных изменений, а более крупные попадут в "фильтрованный" сигнал. Самый типичный пример - попытка усреднить чтение с АЦП средним арифметическим (например для термистора), опросив его просто в цикле несколько раз подряд. Время опроса АЦП на Arduino - сотня микросекунд, то есть такое усреднение уберёт из сигнала высокочастотные шумы порядка 10 кГц. А если у нас шум имеет более низкую частоту, например сетевая наводка в 50 Гц, то такое "усреднение" по сути вообще ничего не даст!
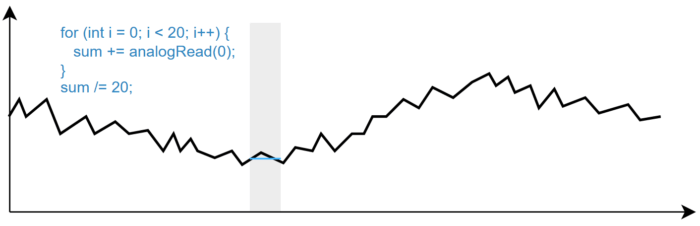
-Видишь усреднение? -Нет. -А оно есть.
Чтобы усреднить такой шум, нужно растянуть выборку хотя бы на пару периодов, т.е. на 40-50 миллисекунд:
Не пара периодов, но уже ближе к делу
Здесь появляется ещё одно понятие - частота среза, она определяет границу между пропускаемыми и ослабляемыми частотами сигнала, т.е. разделяет шум и полезный сигнал:
- Для фильтра низких частот (ФНЧ, LPF) это частота, ниже которой сигналы проходят почти без затухания, а выше - отсекаются фильтром
- Для фильтра высоких частот (ФВЧ, HPF) наоборот, частоты выше среза проходят, а ниже - ослабляются
Как запомнить: фильтр низких частот буквально фильтрует низкие частоты от шума, как фильтр воды фильтрует воду от грязи. В английском варианте (Low Pass Filter) слово Pass означает "пропускать", т.е. фильтр пропускает низкие частоты, а высокие - нет
Все рассмотренные в уроке фильтры являются низкочастотными (ФНЧ), то есть отсекают высокочастотный шум.
Для системы #
Например, тахо-датчик колёсного робота, с которого мы хотим получать скорость вращения колёс. Если опрашивать его слишком редко - скорость не будет соответствовать реальной, а будет накапливаться как некое среднее значение и алгоритмы навигации будут работать некорректно. Если опрашивать слишком часто - значения могут быть слишком шумными или слишком дискретными, особенно если опрашивать чаще, чем тахо-датчик выдаст хотя бы один импульс.
Или для релейного регулятора температуры - если опрашивать датчик температуры слишком редко, то можно пропустить пороговую температуру для выключения реле. Если опрашивать слишком часто, а сигнал шумит - можно заставить реле "дребезжать" и оно быстро выйдет из строя. Но если опрашивать почаще и фильтровать сигнал - будет работать как надо.
Это я к тому, что каждая система индивидуальна и к ней нужно искать свой подход, каких-то средних или универсальных значений не существует.
Среднее арифметическое #
Однократная выборка #
Среднее арифметическое вычисляется как сумма значений, делённая на их количество. Самый простой вариант - однократная выборка, т.е. в цикле получаем сигнал и сразу суммируем, затем делим на количество. Здесь нужно понимать, что работа фильтра напрямую зависит от количества измерений и времени между ними, т.е. от суммарного времени работы фильтра, от окна сигнала, которое он захватит (см. картинку в предыдущей главе). В качестве примера усредним значение с АЦП Arduino:
const int N = 20; // к-во измерений
const int ms = 1; // пауза между ними в мс
float sum = 0;
for (int i = 0; i < N; i++) {
//sum += новое_значение;
sum += analogRead(0);
delay(ms);
}
sum /= N;Особенности:
- Самый лёгкий и математически простой фильтр
- Переменная суммы может быть целочисленной (например
long), но потеряется точность - "Сила" фильтра настраивается размером выборки
Nи паузой между измерениями - Делает несколько измерений за один раз, что может приводить к большим затратам времени
- Блокирующая конструкция с циклом и задержкой - подойдёт не для всех программ
- Запаздывает на размер выборки
Растянутая выборка #
"Асинхронный" вариант предыдущего фильтра. Цикл заменён на набор переменных и функций, нужно вручную передавать новое значение. Пока выборка не завершена - возвращает предыдущий результат. Универсальный класс под любой тип данных:
template <typename T>
class Average {
public:
Average(uint8_t N) : _N(N) {}
T filter(T val) {
_sum += val;
if (++_i == _N) {
_prev = _sum / _N;
_sum = 0;
_i = 0;
}
return _prev;
}
void init(T val) {
_i = 0;
_sum = 0;
_prev = val;
}
private:
T _sum = 0;
T _prev = 0;
const uint8_t _N;
uint8_t _i = 0;
};Average<float> aver(10);
void setup() {
Serial.begin(115200);
aver.init(analogRead(0));
}
void loop() {
Serial.println(aver.filter(analogRead(0)));
delay(50); // или таймер на millis()
}Особенности:
- "Блочное" усреднение, усредняет отдельно каждую выборку
- Асинхронный вариант предыдущего фильтра с циклом
- Запаздывает на размер выборки
Скользящее среднее #
Хранит в буфере несколько последних измерений для усреднения. При каждом вызове фильтра буфер сдвигается, в него добавляется новое значение и убирается самое старое, получается так называемое "окно", которое движется по сигналу. Далее буфер усредняется по среднему арифметическому. Универсальный класс под любой тип данных:
template <typename T, uint8_t N>
class AverageWindow {
public:
float filter(T val) {
_sum += val;
if (++_i >= N) _i = 0;
_sum -= _buffer[_i];
_buffer[_i] = val;
return (float)_sum / N;
}
private:
T _buffer[N] = {};
T _sum = 0;
uint8_t _i = 0;
};AverageWindow<int, 10> aver;
void setup() {
Serial.begin(115200);
}
void loop() {
Serial.println(aver.filter(analogRead(0)));
delay(50); // или таймер на millis()
}Особенности:
- Усредняет последние
Nизмерений, за счёт чего запаздывает. Нуждается в тонкой настройке частоты опроса и размера выборки - Хранит буфер со значениями, что очень неэффективно по сравнению с другими фильтрами

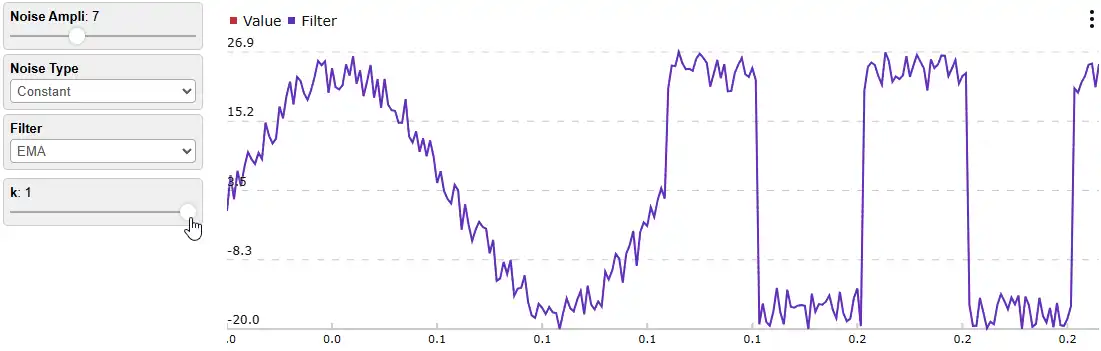
Экспоненциальное бегущее среднее #
Exponential Moving Average, EMA - математически очень простой и достаточно эффективный фильтр. Похож на скользящее среднее, но выглядит более "плавно" за счёт экспоненциального схождения к сигналу (у скользящего среднего оно линейное), что позволяет использовать его не только как фильтр, но и как основу для эффектов и анимаций, а также симуляции плавных процессов.
Классическая формула фильтра:
filter = value * k + filter * (1 - k)filter- фильтрованное значениеvalue- новое значениеk- коэффициент сглаживания от0до1, чем меньше - тем плавнее фильтр
По этой формуле можно понять, как работает фильтр - он складывает фильтрованное и новое значения с разным "весом", сумма весов равна единице. Чем больше в этой взвешенной сумме нового значения, тем более резким будет фильтр, и наоборот
Можно раскрыть скобки и получить более короткую запись:
filter += (value - filter) * kПример:
float k = 0.1; // коэффициент фильтра: 0.0-1.0
float filter = 0; // переменная фильтра
void setup() {
Serial.begin(115200);
}
void loop() {
filter += (analogRead(0) - filter) * k;
Serial.println(filter);
delay(50); // или таймер на millis()
}Или в виде класса:
class EMA {
public:
float filter(float val, float k) {
return _filt += (val - _filt) * k;
}
float filtered() {
return _filt;
}
void init(float val) {
_filt = val;
}
private:
float _filt = 0;
};EMA ema;
void setup() {
Serial.begin(115200);
ema.init(analogRead(0));
}
void loop() {
Serial.println(ema.filter(analogRead(0), 0.3));
delay(50); // или таймер на millis()
}Особенности:
- "Сила" фильтра настраивается коэффициентом и частотой опроса. Чем ниже коэффициент и чем меньше частота - тем плавнее фильтр
- Сильно запаздывает
Выбор коэффициента и dt #
В реальной программе фильтр вызывается с периодом dt, чтобы фильтровать шумы. Я обычно настраиваю фильтр вручную по графику: задаюсь некоторым удобным периодом dt и подгоняю k, пока не станет "хорошо". Но есть и аналитический способ расчёта k и dt: при выборе значения коэффициента k необходимо отталкиваться от того, какие изменения сигнала нам интересны, а какие будем считать за шум.
Через частотные параметры #
k = 1 - exp(-2π * Fc / Fs);
// или без exp()
k = 1 - 1 / (1 + 2π * Fc / Fs);где Fs - частота дискретизации в Гц (обратное значение dt в секундах, т.е. 1 / dt), а Fc - частота среза фильтра в Гц, т.е. до какой частоты сигнал будет проходить через фильтр почти без искажений.
Через постоянную времени #
k = dt / (T + dt);где dt - период дискретизации, а T - постоянная времени, которая отделяет слишком быстрые изменения (шум) от медленных (сигнал), т.е. при значении в 1 секунду фильтр будет пропускать сигнал, который меняется медленнее, чем раз в секунду.
Через длину окна #
k = 2 / (N + 1);где N - ширина окна обычного скользящего среднего (с буфером), т.е. получаем аналогичный ему результат.
Адаптивный коэффициент #
Можно автоматически подстраивать k таким образом, чтобы при больших изменениях сигнала он становился больше (чтобы быстрее догнать сигнал), а при небольших - меньше, чтобы фильтровать статический шум. Это можно делать линейно, например добавим метод в описанный выше класс EMA:
// добавить значение. Вернёт фильтрованное. noise - амплитуда шума, автоматически подстроит k между kMin и kMax
float filter(float val, float noise, float kMin, float kMax) {
float err = (val > _filt) ? (val - _filt) : (_filt - val);
float k = (err >= noise) ? kMax : kMin + (kMax - kMin) * err / noise;
return filter(val, k);
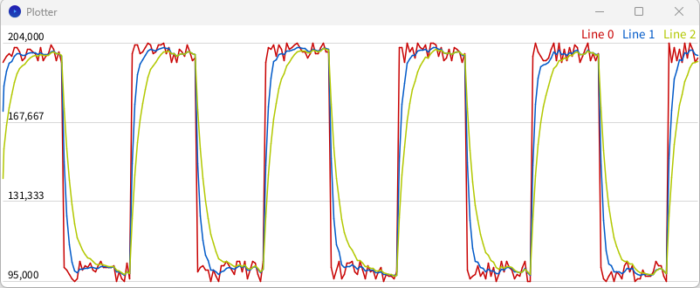
}Результат:
- Красный: сигнал
- Синий: адаптивный
kв диапазоне0.1..0.5 - Зелёный: статичный
k = 0.25
В итоге адаптивный фильтр работает резче при резких изменениях и плавнее на статичном шуме, что даёт гораздо более качественный результат. Минимальный и максимальный k можно прикинуть по описанным выше формулам.
Целочисленный EMA #
Для экономии ресурсов МК (поддержка дробных чисел требует пару килобайт Flash) можно отказаться от float и сделать фильтр целочисленным, для этого все переменные будут целого типа, а вместо умножения на дробный коэффициент будем делить на целое число, например:
fil += (val - fil) / 10; // фильтр с коэффициентом 0.1Да, умножение на float выполнялось бы быстрее деления на 10, но можно заменить деление сдвигом - например фильтр с коэффициентом 1/16 можно записать как
fil += (val - fil) >> 4; // фильтр с коэффициентом 1/16Оптимизировать получится коэффициенты, кратные "степени двойки", то есть 1/2, 1/4, 1/8 и так далее.
Но есть один неприятный момент: в реализации с float у нас в распоряжении огромная точность вычислений и максимальная плавность фильтра, фильтрованное значение со временем полностью совпадёт с текущим. В целочисленной же реализации точность будет ограничена коэффициентом: если разность в скобках (фильтрованное - текущее) будет меньше делителя - переменная фильтра не изменится, так как к ней будет прибавляться 0!
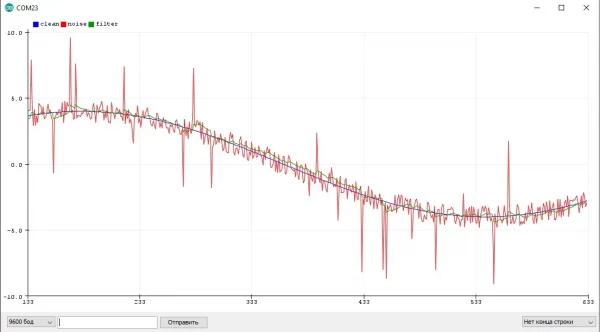
Простой пример: float и целочисленный фильтры "фильтруют" величину от значения 1000 к значению 100 с коэффициентом 0.1 (используем число 10 для наглядности):
fu += (val - fu) / 10;
ff += (val - ff) * 0.1;Где синий график - целочисленный фильтр, красный - float. Из графика видно, что фильтры работают +- одинаково, но вот целочисленный остановился на значении 109, как и ожидалось: в уравнении фильтра получается (100 - 109) / 10, что даёт 0 и переменная фильтра больше не меняется. Эту проблему можно решить двумя способами.
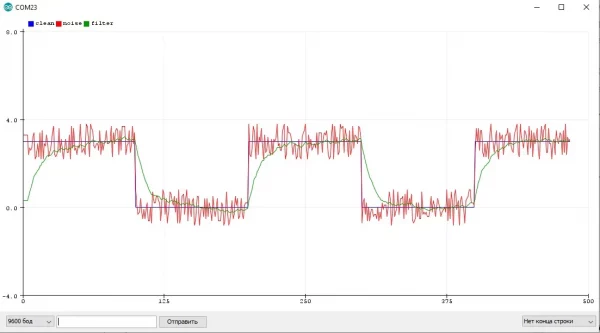
Повышение разрешения #
Искусственно повышаем разрядность фильтра следующим образом: переменная фильтра хранит увеличенное значение и текущее значение мы для вычислений тоже домножаем, а при получении результата - делим, например:
fu += (val * 16 - fu) / 10;
Serial.print(fu / 16);Или на сдвигах:
fu += ((val << 4) - fu) / 10;
Serial.print(fu >> 4);Таким образом, переменная фильтра хранит наше число с 16 кратной точностью, что позволяет в 16 раз увеличить плавность фильтра на критическом участке:
Не забываем, что сдвиг может переполнить два байта и вычисление будет неправильным. Можно заранее прикинуть и подбирать коэффициенты так, чтобы не превышать 2 байта в вычислениях, либо приводить к uint32_t:
fu += (uint32_t)(((uint32_t)val << 4) - fu) >> 5;
Serial.print(fu >> 4);Вычитание ошибки #
Можно использовать следующую конструкцию, которая хранит "ошибку" фильтра и потом учитывает её:
// глобальные или статические
int filt = 0;
int err = 0;
// сам фильтр
int sum = (val - filt) + err;
int div = sum / k;
filt += div;
err = sum - div * k;Универсальный оптимизированный класс быстрого EMA под любой целочисленный тип:
template <typename T>
class IntEMA {
public:
// k2 - коэффициент как степень двойки
T filter(T val, uint8_t k2) {
T sum = (val - _filt) + _err;
T div = sum >> k2;
_err = sum - (div << k2);
return _filt += div;
}
void init(T val) {
_filt = val;
_err = 0;
}
T filtered() {
return _filt;
}
private:
T _filt = 0, _err = 0;
};Здесь k2 превратится в степень двойки, т.е. 1 это фильтр 1/2, 3 - 1/8 и так далее, чем больше k2 - тем плавнее фильтр:
IntEMA<int> ema1;
IntEMA<int> ema2;
void setup() {
Serial.begin(115200);
ema1.init(analogRead(0));
ema2.init(analogRead(0));
}
void loop() {
ema1.filter(analogRead(0), 1);
ema2.filter(analogRead(0), 3);
Serial.print(analogRead(0));
Serial.print(',');
Serial.print(ema1.filtered());
Serial.print(',');
Serial.println(ema2.filtered());
delay(50); // или таймер на millis()
}Ещё пара вариантов #
Идея взята из статьи на easyelectronics:
filt = (A * filt + B * signal) >> k;Коэффициенты выбираются следующим образом:
k= 1, 2, 3...A + B = 2^k- Чем больше
А, тем плавнее фильтр (отношение A/B) - Чем больше
k, тем более плавным можно сделать фильтр. Но больше 5 уже нет смысла, т.к.A=31,B=1уже очень плавно, а при увеличении может переполнитьсяintи придётся использовать 32-х битные типы данных. - Результат умножения не должен выходить за
int, иначе придётся преобразовывать кlong - Более подробно о выборе коэффициентов читайте в статье, ссылка выше
- Особенность: если "ошибка" сигнала
(signal – filter) меньше 2^k- фильтрованное значение меняться не будет. Для повышения "разрешения" фильтра можно домножить (или сдвинуть) переменную фильтра, то есть фильтровать в бОльших величинах
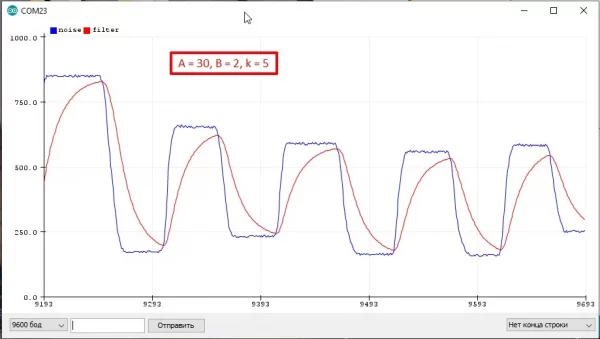
Например k = 4, значит A+B = 16. Хотим плавный фильтр, принимаем A=14, B=2: filt = (14 * filt + 2 * signal) >> 4:
Далее коэффициент B можно принять за 1 и сэкономить одно умножение:
filt = (A * filt + signal) >> k;Тогда коэффициенты выбираются как:
k= 1, 2, 3...A = (2^k) - 1- [k=2 A=3], [k=3 A=7], [k=4 A=15], [k=5 A=31]...- Чем больше
k, тем плавнее фильтр
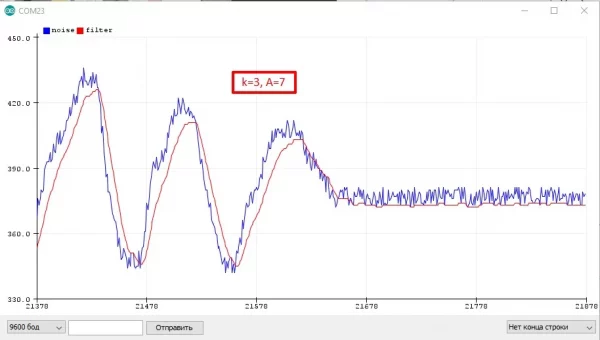
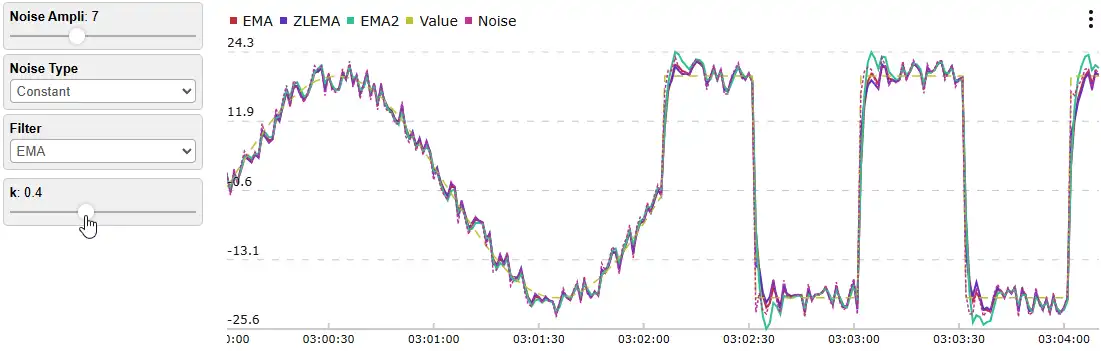
ZLEMA #
Zero Lag EMA - модифицированный EMA фильтр, в котором уменьшено отставание от реального сигнала:
class ZLEMA {
public:
float filter(float val, float k) {
_filt += ((2 * val - _prev) - _filt) * k;
_prev = val;
return _filt;
}
void init(float val) {
_filt = val;
_prev = val;
}
private:
float _filt = 0;
float _prev = 0;
};ZLEMA zlema;
void setup() {
Serial.begin(115200);
zlema.init(analogRead(0));
}
void loop() {
Serial.println(zlema.filter(analogRead(0), 0.3));
delay(50); // или таймер на millis()
}На деле он не сильно лучше обычного EMA:
EMA2 #
Ещё одна модификация EMA - двойное экспоненциальное сглаживание, имеет уменьшенное отставание по сравнению с обычным EMA:
class EMA2 {
public:
float filter(float val, float k) {
_filt1 += (val - _filt1) * k;
_filt2 += (_filt1 - _filt2) * k;
return 2 * _filt1 - _filt2;
}
void init(float val) {
_filt1 = _filt2 = val;
}
private:
float _filt1 = 0, _filt2 = 0;
};EMA2 ema;
void setup() {
Serial.begin(115200);
ema.init(analogRead(0));
}
void loop() {
Serial.println(ema.filter(analogRead(0), 0.3));
delay(50); // или таймер на millis()
}Особенности:
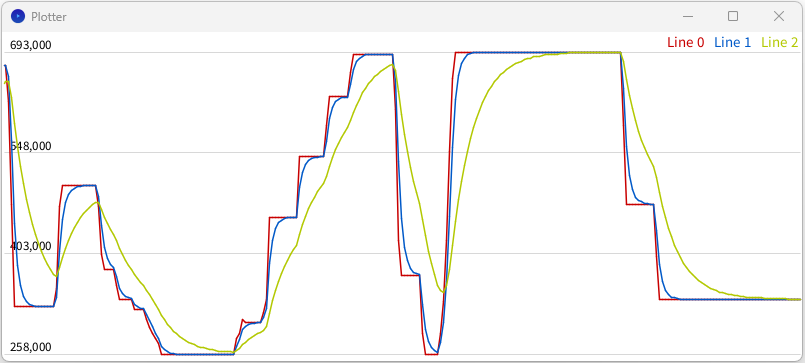
- Действительно меньше отстаёт, но хорошо работает только на плавном сигнале - резкие изменения сигнала приводят к "забросам" (т.к. алгоритм "догоняет" несуществующий сгинал), это видно на части графика с квадратным сигналом
Super Smooth #
Сглаживающий ФНЧ фильтр Эхлера. Похож на EMA, но меньше отстаёт при похожем уровне сглаживания. Удобно настраивается по частотам:
class SSF {
public:
void init(float val) {
_y1 = _y2 = val;
}
// f_cut - частота среза
// f_discr - частота дискретизации
void config(float f_cut, float f_discr) {
float x = exp(-2.0 * 3.1415 * f_cut / f_discr);
_b0 = 1.0 - 2.0 * x + x * x;
_a1 = 2 * x;
_a2 = -x * x;
}
float filter(float val) {
float y = _b0 * val + _a1 * _y1 + _a2 * _y2;
_y2 = _y1;
_y1 = y;
return y;
}
private:
float _b0 = 0, _a1 = 0, _a2 = 0;
float _y1 = 0, _y2 = 0;
};SSF ssf;
void setup() {
Serial.begin(115200);
ssf.config(4, 1 / 0.05);
ssf.init(analogRead(0));
}
void loop() {
Serial.println(ssf.filter(analogRead(0)));
delay(50); // или таймер на millis()
}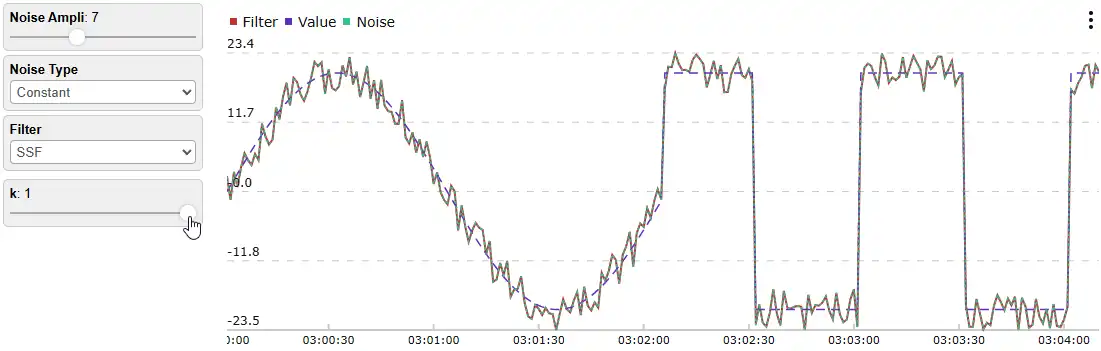
Здесь для демонстрации я задаю коэффициент как условный k, выразив через него частоту
Простой Калман #
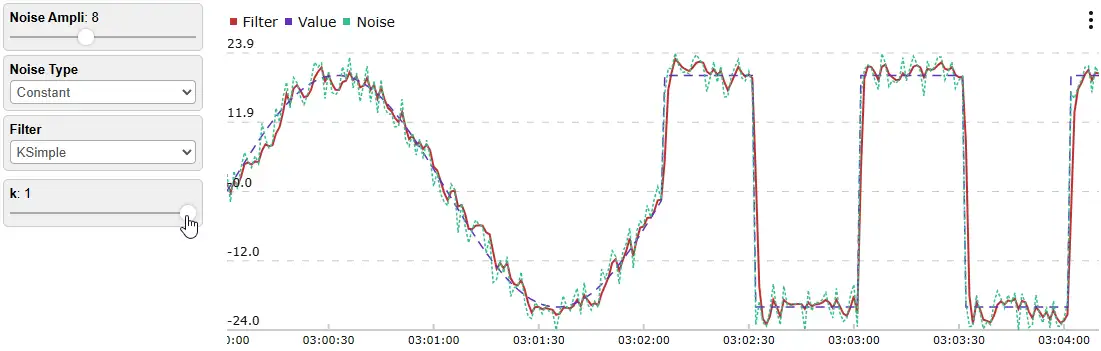
Реализация одномерного упрощённого фильтра Калмана, предсказывает текущее значение на основе прошлого и оценки ошибки. Сам подстраивается под сигнал в процессе работы.
class KSimple {
public:
void init(float val) {
_last_est = val;
}
// стд. отклонение шума
void config(float stddev_noise) {
_noise = stddev_noise;
_err_est = stddev_noise;
_last_est = 0;
}
// k - коэффициент силы фильтра
float filter(float val, float k) {
float gain = _err_est / (_err_est + _noise);
float est = _last_est + gain * (val - _last_est);
_err_est = (1.0 - gain) * _err_est + abs(_last_est - est) * k;
_last_est = est;
return est;
}
private:
float _noise = 0;
float _err_est = 0;
float _last_est = 0;
};KSimple ks;
void setup() {
Serial.begin(115200);
ks.init(analogRead(0));
ks.config(3);
}
void loop() {
Serial.println(ks.filter(analogRead(0), 0.3));
delay(50); // или таймер на millis()
}stddev_noise- стандартное отклонение шума. Можно задать как амплитуду шума, делённую на3. Амплитуду шума можно замерить "на глаз" по графикуk— коэффициент силы фильтра, регулирует скорость адаптации оценки ошибки. Чем меньше - тем плавнее фильтр, при правильной настройке стандартного отклонения коэффициентkбудет лежать в диапазоне 0.0.. 1.0, но может быть и больше
Особенности:
- Хорошо фильтрует как постоянный шум, так и резкие выбросы
- Запаздывает меньше, чем бегущее среднее
- Подстраивается под сигнал в процессе работы
- Расчёт длится ~90 мкс (AVR, 16 МГц)
- Точно указывать
stddev_noiseне обязательно: по сути он работает совместно сkи фильтр в любом случае настраивается поk- для разныхstddev_noiseбудет разныйk

Альфа-Бета фильтр #
AB фильтр тоже является одним из видов фильтра Калмана, подробнее можно почитать можно на Википедии:
class ABFilt {
public:
void init(float val) {
_xk_1 = _vk_1 = val;
}
// период фильтрации
// стд. отклонение шума измерений (ошибка датчика)
// стд. отклонение процесса (изменения в состоянии)
void config(float dt, float stddev_process, float stddev_noise) {
float lambda = dt * dt * stddev_process / stddev_noise;
float r = (4 + lambda - sqrt(8 * lambda + lambda * lambda)) / 4;
_a = 1 - r * r;
_b = 2 * (2 - _a) - 4 * sqrt(1 - _a);
_dt = dt;
_xk_1 = 0;
_vk_1 = 0;
}
float filter(float val) {
float xk = _xk_1 + _vk_1 * _dt;
float vk = _vk_1;
float rk = val - xk;
xk += _a * rk;
vk += (_b * rk) / _dt;
_xk_1 = xk;
_vk_1 = vk;
return _xk_1;
}
private:
float _a = 0, _b = 0;
float _dt = 0;
float _xk_1 = 0, _vk_1 = 0;
};ABFilt ab;
void setup() {
Serial.begin(115200);
ab.init(analogRead(0));
ab.config(0.05, 5, 1);
}
void loop() {
Serial.println(ab.filter(analogRead(0)));
delay(50); // или таймер на millis()
}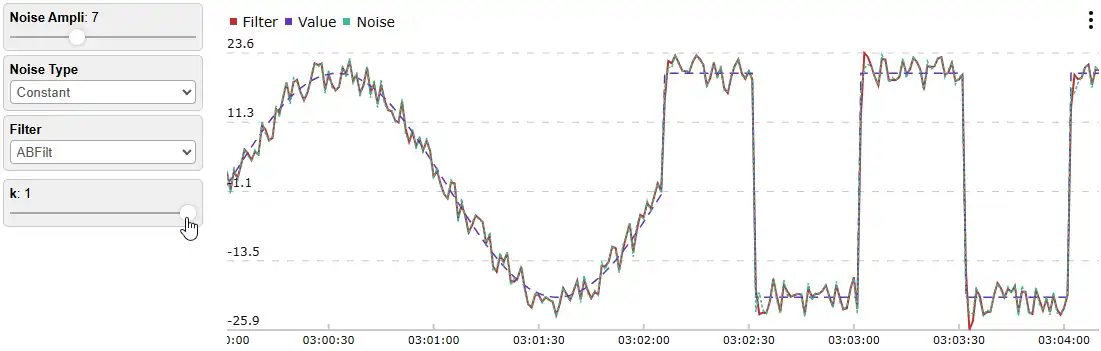
Примечание: здесь задаётся "общий" коэффициент, для фильтра, т.к. в вычислениях все настройки сводятся в одну
Особенности:
- Хорошо показывает себя на гладких сигналах
- На ступенчатых сигналах или при резком изменении даёт "заброс" по значению
Метод наименьших квадратов #
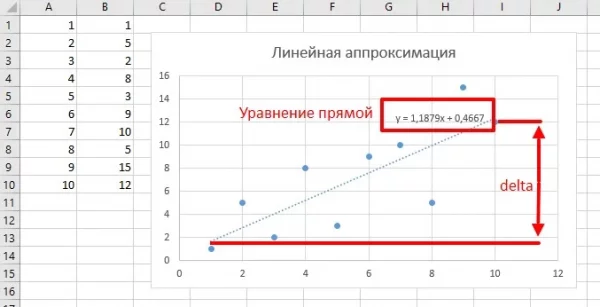
Следующий фильтр позволяет наблюдать за шумным процессом и предсказывать его поведение - теория есть тут. Чисто графическое объяснение здесь такое: у нас есть набор данных в виде нескольких точек на плоскости. Мы видим, что общее направление идёт на увеличение, но шум не позволяет сделать точный вывод или прогноз на дальнейшее направление. Предположим, что существует линия, сумма квадратов расстояний от каждой точки до которой - минимальна. Такая линия будет наиболее точно показывать реальное изменение сигнала, в этом и заключается метод наименьших квадратов.
Следующий класс выдает параметры прямой линии, которая равноудалена от всех точек на плоскости (задаются двумя массивами), по сути - линейная аппроксимация:
class MinQuad {
public:
// тип вычислений, тип массивов
template <typename Ts, typename Tx, typename Ty>
void compute(Tx *x_array, Ty *y_array, size_t len) {
Ts sumX = 0, sumY = 0, sumX2 = 0, sumXY = 0;
for (size_t i = 0; i < len; i++) {
sumX += x_array[i];
sumY += y_array[i];
sumX2 += (Ts)x_array[i] * x_array[i];
sumXY += (Ts)x_array[i] * y_array[i];
}
a = (float)(len * sumXY - sumX * sumY) / (len * sumX2 - sumX * sumX);
b = (float)(sumY - a * sumX) / len;
delta = a * (x_array[len - 1] - x_array[0]);
}
// получить коэффициент А
float getA() {
return a;
}
// получить коэффициент В
float getB() {
return b;
}
// получить аппроксимированное изменение
float getDelta() {
return delta;
}
private:
float a, b, delta;
};Нужно указать тип данных, который будет использован для промежуточных вычислений - в расчётах будет использована сумма квадратов, поэтому тип должен быть достаточным, чтобы вместить результат. Если сами массивы int, то тип нужно взять long или float, а для массивов float можно просто использовать float.
void setup() {
Serial.begin(115200);
int x_array[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int y_array[] = {1, 5, 2, 8, 3, 9, 10, 5, 15, 12};
MinQuad mq;
mq.compute<long>(x_array, y_array, 10);
// Уравнение вида у = A*x + B
Serial.println(mq.getA()); // получить коэффициент А
Serial.println(mq.getB()); // получить коэффициент В
Serial.println(mq.getDelta()); // получить изменение (аппроксимированное)
// A=1.19, B=0.47, D=10.69
}
void loop() {
}Хорошо подходит для определения тренда, например понижение или повышение атмосферного давления по барометру.
Медианный фильтр #
Медианный фильтр тоже находит среднее значение, но не усредняя, а выбирая его из представленных.
Порядка 3 #
Алгоритм для медианы 3-го порядка (выбор из трёх значений) можно записать так:
int median3(int a, int b, int c) {
return (a < b) ? ((b < c) ? b : ((c < a) ? a : c)) : ((a < c) ? a : ((c < b) ? b : c));
}Для удобства и потокового использования можно сделать класс под любой тип данных, который будет хранить в себе циклический буфер на последние три значения и автоматически добавлять в него новые:
template <typename T>
class Median3 {
public:
T filter(T val) {
if (++_i >= 3) _i = 0;
_buf[_i] = val;
return getMedian(_buf[0], _buf[1], _buf[2]);
}
void init(T val) {
_buf[0] = _buf[1] = _buf[2] = val;
}
static inline T getMedian(T a, T b, T c) {
return (a < b) ? ((b < c) ? b : ((c < a) ? a : c)) : ((a < c) ? a : ((c < b) ? b : c));
}
private:
T _buf[3] = {};
uint8_t _i = 0;
};Median3<int> med;
void setup() {
Serial.begin(115200);
med.init(analogRead(0));
}
void loop() {
Serial.println(med.filter(analogRead(0)));
delay(50); // или таймер на millis()
}Также можно вызывать как независимую функцию для трёх переменных:
Median3<int>::getMedian(1, 2, 3); // вернёт 2Особенности:
- Медиана отлично фильтрует резкие единичные изменения значения - буквально игнорирует их
- Самый быстрый фильтр - отсутствуют вычисления, есть только выбор
- Реализация для 3 порядка - очень простая
- Запаздывает на половину размерности фильтра
Порядка N #
Медианный фильтр для любой размерности можно написать так:
// оптимальный вариант медианы для N значений
// предложен Виталием Емельяновым, доработан AlexGyver
template <typename T, uint8_t N>
class MedianN {
public:
T filter(T val) {
_buf[_i] = val;
if ((_i < N - 1) && (_buf[_i] > _buf[_i + 1])) {
for (uint8_t i = _i; i < N - 1; i++) {
if (_buf[i] > _buf[i + 1]) {
T t = _buf[i];
_buf[i] = _buf[i + 1];
_buf[i + 1] = t;
}
}
} else {
if ((_i > 0) && (_buf[_i - 1] > _buf[_i])) {
for (uint8_t i = _i; i > 0; i--) {
if (_buf[i] < _buf[i - 1]) {
T t = _buf[i];
_buf[i] = _buf[i - 1];
_buf[i - 1] = t;
}
}
}
}
if (++_i >= N) _i = 0;
return _buf[N / 2];
}
void init(T val) {
for (uint8_t i = 0; i < N; i++) _buf[i] = val;
}
private:
T _buf[N];
uint8_t _i = 0;
};MedianN<int, 10> med;
void setup() {
Serial.begin(115200);
med.init(analogRead(0));
}
void loop() {
Serial.println(med.filter(analogRead(0)));
delay(50); // или таймер на millis()
}Особенности:
- Запаздывает на половину размерности
- Отсеивает даже несколько пиков подряд, если ширина выброса меньше половины размерности фильтра
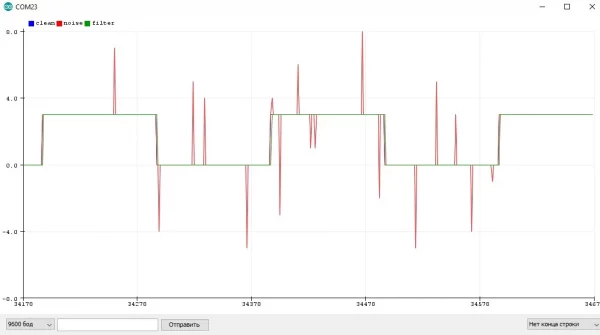
Пиковый фильтр #
Данный фильтр был разработан мной в качестве первой ступени фильтрации для датчика расстояния - сигнал с него может содержать резкие пики, одиночные или несколько подряд, они сводят с ума почти любой "сглаживающий" фильтр. Такая ситуация обычно наблюдается на границе движущегося объекта, когда датчик может видеть и не видеть его от измерения к измерению. С таким сигналом хорошо работает медианный фильтр, но медианы из трёх недостаточно, а медиана из N - "дорогая" по памяти и сложнее настраивается.
Суть фильтра состоит в том, что он игнорирует новое значение, если оно отличается от предыдущего меньше, чем на указанный порог thrsh. Но если таких значений подряд становится больше указанного количества n - фильтр принимает это значение и по сути переходит в новый диапазон. Универсальный класс такого фильтра:
template <typename T>
class PeakFilter {
public:
void init(T val) {
_filt = _raw = val;
_count = 0;
}
// порог, кол-во значений
void config(T thrsh, uint8_t n) {
_thrsh = thrsh;
_n = n;
}
T filter(T val) {
_raw = val;
T diff = (val > _filt) ? (val - _filt) : (_filt - val);
if (diff > _thrsh) {
if (++_count >= _n) {
_filt = val;
_count = 0;
}
} else {
_filt = val;
_count = 0;
}
return _filt;
}
T filtered() {
return _filt;
}
private:
T _filt = 0;
T _raw = 0;
T _thrsh = 100;
uint8_t _n = 3;
uint8_t _count = 0;
};PeakFilter<int> peak;
void setup() {
Serial.begin(115200);
peak.config(100, 3);
peak.init(analogRead(0));
}
void loop() {
Serial.println(peak.filter(analogRead(0)));
delay(50); // или таймер на millis()
}Особенности:
- Игнорирует резкие изменения сигнала на величину меньше порога
thrsh, пока изменение не станет постоянным - Нулевое запаздывание на гладком сигнале
- Запаздывание на ступенчатом сигнале равно настройке фильтра
n - Хорошо работает как первая "грубая" ступень фильтрации
Какой фильтр выбрать? #
Выбор фильтра зависит от типа сигнала и ограничений по времени фильтрации. Среднее арифметическое – хорошо подходит, если фильтрации производятся редко и время одного измерения значения мало. Для большинства ситуаций подходит бегущее среднее EMA и его модификации - он довольно быстрый и даёт хороший результат при правильной настройке. Медианный фильтр 3-го порядка тоже очень быстрый, но он может только отсеить выбросы, сам сигнал он не сгладит, поэтому хорошо работает в паре с EMA. Упрощённый Калман – отличный фильтр, справляется с любым типом шума, имея малое отставание от сигнала по фазе. Линейная аппроксимация наименьшими квадратами – инструмент специального назначения, позволяющий буквально предсказывать поведение значения за период - получаем уравнение прямой. Если нужно максимальное быстродействие - работаем только с целыми числами и используем целочисленные фильтры, например тот же EMA.
Дополнительно #
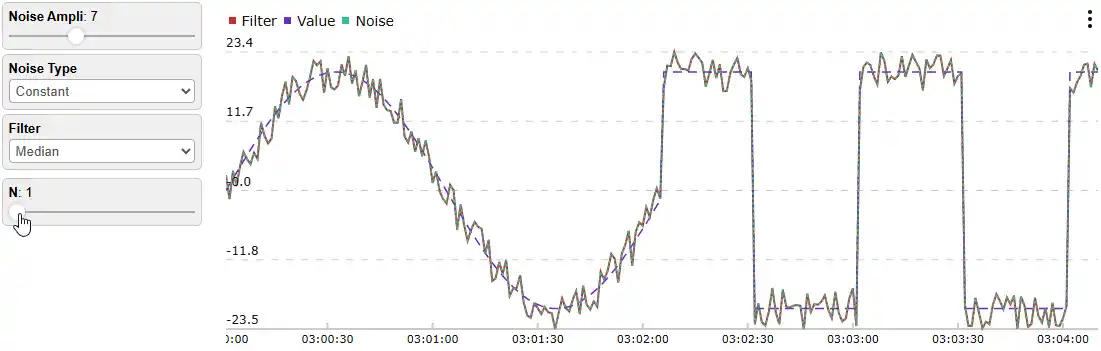
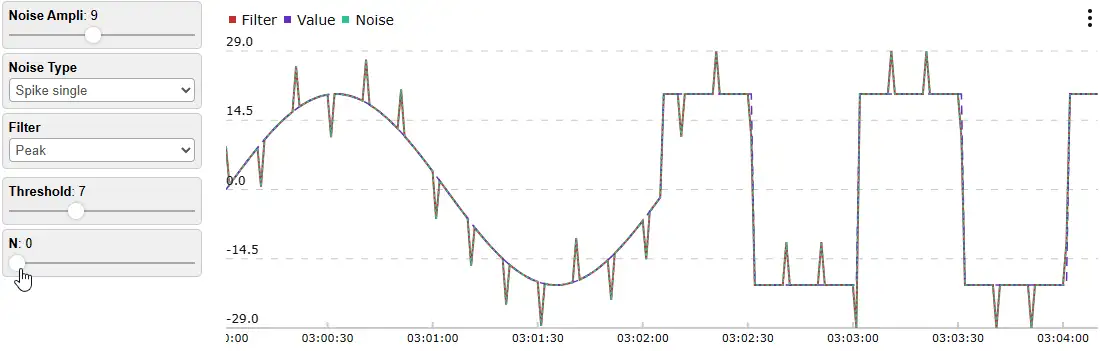
Дополнительный контент доступен владельцам набора GyverKIT и по подписке, подробнее читай здесь. Блок содержит:
- Интерактивный график
Полезные страницы #
- Набор GyverKIT – наш большой стартовый набор Arduino, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])
- Поддержать автора за работу над уроками